Google
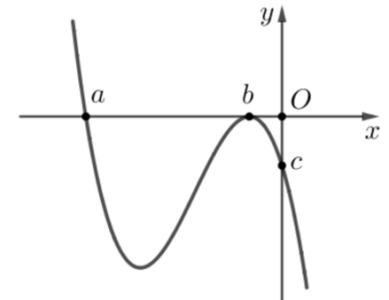
Câu hỏi: Xét các số thực âm $a,b,c$ sao cho hàm số bậc ba $f\left( x \right)$ có đồ thị như hình vẽ bên:
Hàm số $g\left( x \right)=\left| f\left( xf\left( x \right) \right)-c \right|$ có bao nhiêu điểm cực trị?
A. 15.
B. 14.
C. 11.
D. 13.
A. 15.
B. 14.
C. 11.
D. 13.
Xét hàm số $u\left( x \right)=f\left( xf\left( x \right) \right)-c\Rightarrow g\left( x \right)=\left| u\left( x \right) \right|$ ta đếm số lần đổi dấu của $u\left( x \right)$ và ${u}'\left( x \right)$.
Ta có $f\left( x \right)=k\cdot \left( x-a \right){{(x-b)}^{2}}$, ( $\left. \text{li}{{\text{m}}_{x\to +\infty }}f\left( x \right)=-\infty \Rightarrow k<0 \right)$ và có hai điểm cực trị $x=m;x=b$.
Đường thẳng $y=c$ cắt đồ thị $f\left( x \right)$ tại ba điểm phân biệt có hoành độ $\alpha ;\beta ;0$ nên $f\left( x \right)-c=k\cdot x\left( x-\alpha \right)\left( x-\beta \right)\Rightarrow u\left( x \right)=k.xf\left( x \right)\left( xf\left( x \right)-\alpha \right)\left( xf\left( x \right)-\beta \right)$
Ta có $xf\left( x \right)$ đổi dấu khi qua các điểm $x=0;x=a$ và các phương trình $xf\left( x \right)=\alpha \Leftrightarrow f\left( x \right)=\dfrac{\alpha }{x};xf\left( x \right)=\beta \Leftrightarrow f\left( x \right)=\dfrac{\beta }{x}$ mỗi phương trình có hai nghiệm phân biệt.
Nên $u\left( x \right)$ có $2+2+2=6$ lần đổi dấu
Xét ${u}'\left( x \right)=\left( f\left( x \right)+x{f}'\left( x \right) \right)\cdot {f}'\left( xf\left( x \right) \right)=0\Leftrightarrow \left[ \begin{matrix}
f\left( x \right)+x{f}'\left( x \right)=0 \\
xf\left( x \right)=m \\
xf\left( x \right)=b \\
\end{matrix} \right.$
Mỗi phương trình $xf\left( x \right)=m\Leftrightarrow f\left( x \right)=\dfrac{m}{x};xf\left( x \right)=b\Leftrightarrow f\left( x \right)=\dfrac{b}{x}$ có hai nghiệm phân biệt
Và $f\left( x \right)+x{f}'\left( x \right)=k\left( x-a \right){{(x-b)}^{2}}+kx\cdot \left[ {{(x-b)}^{2}}+2\left( x-a \right)\left( x-b \right) \right]$
$=k\left( x-b \right)\left[ \left( x-a \right)\left( x-b \right)+x\left( 3x-2a-b \right) \right]=k\left( x-b \right)\left[ 4{{x}^{2}}-\left( 3a+2b \right)x+ab \right]$ có ba nghiệm phân biệt.
Nên ${u}'\left( x \right)$ có $3+2+2=7$ lần đổi dấu. Do đó $u\left( x \right)$ có 7 điểm cực trị. Vậy hàm số $g\left( x \right)=\left| u\left( x \right) \right|$ có $6+7=13$ điểm cực trị.
Ta có $f\left( x \right)=k\cdot \left( x-a \right){{(x-b)}^{2}}$, ( $\left. \text{li}{{\text{m}}_{x\to +\infty }}f\left( x \right)=-\infty \Rightarrow k<0 \right)$ và có hai điểm cực trị $x=m;x=b$.
Đường thẳng $y=c$ cắt đồ thị $f\left( x \right)$ tại ba điểm phân biệt có hoành độ $\alpha ;\beta ;0$ nên $f\left( x \right)-c=k\cdot x\left( x-\alpha \right)\left( x-\beta \right)\Rightarrow u\left( x \right)=k.xf\left( x \right)\left( xf\left( x \right)-\alpha \right)\left( xf\left( x \right)-\beta \right)$
Ta có $xf\left( x \right)$ đổi dấu khi qua các điểm $x=0;x=a$ và các phương trình $xf\left( x \right)=\alpha \Leftrightarrow f\left( x \right)=\dfrac{\alpha }{x};xf\left( x \right)=\beta \Leftrightarrow f\left( x \right)=\dfrac{\beta }{x}$ mỗi phương trình có hai nghiệm phân biệt.
Xét ${u}'\left( x \right)=\left( f\left( x \right)+x{f}'\left( x \right) \right)\cdot {f}'\left( xf\left( x \right) \right)=0\Leftrightarrow \left[ \begin{matrix}
f\left( x \right)+x{f}'\left( x \right)=0 \\
xf\left( x \right)=m \\
xf\left( x \right)=b \\
\end{matrix} \right.$
Mỗi phương trình $xf\left( x \right)=m\Leftrightarrow f\left( x \right)=\dfrac{m}{x};xf\left( x \right)=b\Leftrightarrow f\left( x \right)=\dfrac{b}{x}$ có hai nghiệm phân biệt
Và $f\left( x \right)+x{f}'\left( x \right)=k\left( x-a \right){{(x-b)}^{2}}+kx\cdot \left[ {{(x-b)}^{2}}+2\left( x-a \right)\left( x-b \right) \right]$
$=k\left( x-b \right)\left[ \left( x-a \right)\left( x-b \right)+x\left( 3x-2a-b \right) \right]=k\left( x-b \right)\left[ 4{{x}^{2}}-\left( 3a+2b \right)x+ab \right]$ có ba nghiệm phân biệt.
Nên ${u}'\left( x \right)$ có $3+2+2=7$ lần đổi dấu. Do đó $u\left( x \right)$ có 7 điểm cực trị. Vậy hàm số $g\left( x \right)=\left| u\left( x \right) \right|$ có $6+7=13$ điểm cực trị.
Đáp án D.