Google
Câu hỏi: Xét các số phức $z$, $w$ thỏa mãn $\left| z-1 \right|=\left| z-i \right|$ và $\left| w-4i \right|=1$. Giá trị nhỏ nhất của $\left| z-w \right|$ bằng
A. $2\sqrt{2}+1$.
B. $2$.
C. $3$.
D. $2\sqrt{2}-1$.
A. $2\sqrt{2}+1$.
B. $2$.
C. $3$.
D. $2\sqrt{2}-1$.
Đặt $z=x+yi$ với $x,y\in \mathbb{R}$.
Ta có: $\left| z-1 \right|=\left| z-i \right|\Rightarrow {{\left( x-1 \right)}^{2}}+{{y}^{2}}={{x}^{2}}+{{\left( y-1 \right)}^{2}}\Leftrightarrow x-y=0$ do đó tập hợp các điểm biểu diễn số phức $z$ là đường thẳng $d:x-y=0$.
Lại có: $\left| w-4i \right|=1$ nên tập hợp các điểm biểu diễn số phức $w$ là đường tròn $\left( C \right)$ có tâm $I\left( 0;4 \right)$ và bán kính $R=1$.
Gọi $A$ là điểm biểu diễn của số phức $z$ và $B$ là điểm biểu diễn của số phức $w$ khi đó
$\left| z-w \right|=AB$ như vậy $\left| z-w \right|$ nhỏ nhất khi $AB$ nhỏ nhất.
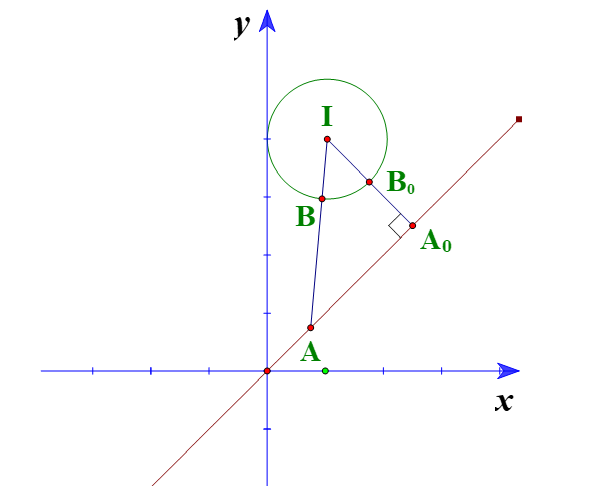Quan sát hình vẽ, nhận thấy: $AB$ nhỏ nhất khi $A$ trùng ${{A}_{0}}$ và $B$ trùng với ${{B}_{0}}$.
Khi đó: $I{{B}_{0}}=1$ và $I{{A}_{0}}=d\left( I,d \right)=\dfrac{\left| 0-4 \right|}{\sqrt{{{1}^{2}}+{{\left( -1 \right)}^{2}}}}=2\sqrt{2}$ do vậy $A{{B}_{\min }}=2\sqrt{2}-1$.
Vậy giá trị nhỏ nhất của $\left| z-w \right|$ bằng $2\sqrt{2}-1$.
Ta có: $\left| z-1 \right|=\left| z-i \right|\Rightarrow {{\left( x-1 \right)}^{2}}+{{y}^{2}}={{x}^{2}}+{{\left( y-1 \right)}^{2}}\Leftrightarrow x-y=0$ do đó tập hợp các điểm biểu diễn số phức $z$ là đường thẳng $d:x-y=0$.
Lại có: $\left| w-4i \right|=1$ nên tập hợp các điểm biểu diễn số phức $w$ là đường tròn $\left( C \right)$ có tâm $I\left( 0;4 \right)$ và bán kính $R=1$.
Gọi $A$ là điểm biểu diễn của số phức $z$ và $B$ là điểm biểu diễn của số phức $w$ khi đó
$\left| z-w \right|=AB$ như vậy $\left| z-w \right|$ nhỏ nhất khi $AB$ nhỏ nhất.
Khi đó: $I{{B}_{0}}=1$ và $I{{A}_{0}}=d\left( I,d \right)=\dfrac{\left| 0-4 \right|}{\sqrt{{{1}^{2}}+{{\left( -1 \right)}^{2}}}}=2\sqrt{2}$ do vậy $A{{B}_{\min }}=2\sqrt{2}-1$.
Vậy giá trị nhỏ nhất của $\left| z-w \right|$ bằng $2\sqrt{2}-1$.
Đáp án D.