Google
Câu hỏi: Từ một tấm bạt hình chữ nhật có kích thước $12m \times 6m$ như hình vẽ. Một nhóm học sinh trong quá trình đi dã ngoại đã gập đôi tấm bạt lại theo đoạn nối trung điểm 2 cạnh là chiều rộng của tấm bạt sao cho 2 mép chiều dài của tấm bạt sát đất và cách nhau $x (m)$ (như hình vẽ). Tìm x để khoảng không gian trong lều là lớn nhất.
A. $x=4$.
B. $x=3\sqrt{2}$.
C. $x=3$.
D. $x=3\sqrt{3}$.
B. $x=3\sqrt{2}$.
C. $x=3$.
D. $x=3\sqrt{3}$.
Phần không gian trong lều được tính bởi công thức thể tích hình lăng trụ đứng.
Ta có: $V=h.{{S}_{\Delta ABC}}=12.{{S}_{\Delta ABC}}$. Như vậy để thể tích lớn nhất khi diện tích tam giác đáy $ABC$ là lớn nhất. Trong tam giác đáy $ABC$, vẽ đường cao $AH$. Ta có $AH=\sqrt{9-\dfrac{{{x}^{2}}}{4}}.$
Do đó diện tích: ${{S}_{\Delta ABC}}=\dfrac{1}{2}x.\sqrt{9-\dfrac{{{x}^{2}}}{4}}=\dfrac{1}{4}x\sqrt{36-{{x}^{2}}}.$
Xét hàm $S(x)=\dfrac{1}{4}x\sqrt{36-{{x}^{2}}}$ với $x\in (0;6);$
${S}'(x)=\dfrac{1}{4}\left( \sqrt{36-{{x}^{2}}}+x\dfrac{-x}{\sqrt{36-{{x}^{2}}}} \right)=\dfrac{1}{4}.\dfrac{36-{{x}^{2}}-{{x}^{2}}}{\sqrt{36-{{x}^{2}}}}$.
${S}'(x)=0\Leftrightarrow 36-2{{x}^{2}}=0\Leftrightarrow x=3\sqrt{2}.$
Bảng biến thiên:
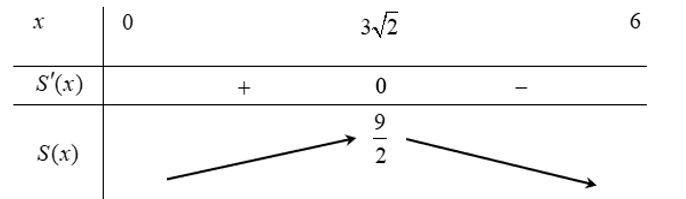Vậy với $x=3\sqrt{2}\left( m \right)$ thì thể tích lều là lớn nhất.
Ta có: $V=h.{{S}_{\Delta ABC}}=12.{{S}_{\Delta ABC}}$. Như vậy để thể tích lớn nhất khi diện tích tam giác đáy $ABC$ là lớn nhất. Trong tam giác đáy $ABC$, vẽ đường cao $AH$. Ta có $AH=\sqrt{9-\dfrac{{{x}^{2}}}{4}}.$
Do đó diện tích: ${{S}_{\Delta ABC}}=\dfrac{1}{2}x.\sqrt{9-\dfrac{{{x}^{2}}}{4}}=\dfrac{1}{4}x\sqrt{36-{{x}^{2}}}.$
Xét hàm $S(x)=\dfrac{1}{4}x\sqrt{36-{{x}^{2}}}$ với $x\in (0;6);$
${S}'(x)=\dfrac{1}{4}\left( \sqrt{36-{{x}^{2}}}+x\dfrac{-x}{\sqrt{36-{{x}^{2}}}} \right)=\dfrac{1}{4}.\dfrac{36-{{x}^{2}}-{{x}^{2}}}{\sqrt{36-{{x}^{2}}}}$.
${S}'(x)=0\Leftrightarrow 36-2{{x}^{2}}=0\Leftrightarrow x=3\sqrt{2}.$
Bảng biến thiên:
Đáp án B.