Google
Câu hỏi: Từ một khối gỗ dạng khối lăng trụ đứng $ABC.A'B'C'$ có $AB=30cm,BC=40cm,CA=50cm$ và chiều cao $AA'=100cm;$ người ta tiện để thu được một khối trụ có cùng chiều cao với khối gỗ ban đầu và đường tròn đáy là đường tròn nội tiếp tam giác $ABC$. Thể tích của khối trụ gần nhất với giá trị nào dưới đây?
A. $62500c{{m}^{3}}$.
B. $60000c{{m}^{3}}$.
C. $31416c{{m}^{3}}$.
D. $6702c{{m}^{3}}$.
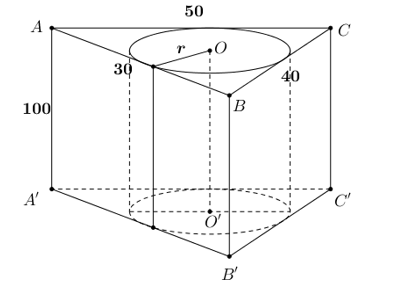Xét tam giác $ABC$ có: $C{{A}^{2}}=B{{A}^{2}}+B{{C}^{2}}$ nên tam giác $ABC$ vuông tại $B$.
Gọi $r$ là bán kính đường tròn nội tiếp tam giác $ABC$ ta có:
$r=\dfrac{{{S}_{\Delta ABC}}}{p}=\dfrac{\dfrac{1}{2}BA.BC}{\dfrac{1}{2}(BA+BC+CA)}=\dfrac{30.40}{30+40+50}=10cm$.
Thể tích khối trụ là: $V=\pi {{r}^{2}}.h=\pi {{.10}^{2}}.100=10000\pi \approx 31416c{{m}^{3}}$.
A. $62500c{{m}^{3}}$.
B. $60000c{{m}^{3}}$.
C. $31416c{{m}^{3}}$.
D. $6702c{{m}^{3}}$.
Gọi $r$ là bán kính đường tròn nội tiếp tam giác $ABC$ ta có:
$r=\dfrac{{{S}_{\Delta ABC}}}{p}=\dfrac{\dfrac{1}{2}BA.BC}{\dfrac{1}{2}(BA+BC+CA)}=\dfrac{30.40}{30+40+50}=10cm$.
Thể tích khối trụ là: $V=\pi {{r}^{2}}.h=\pi {{.10}^{2}}.100=10000\pi \approx 31416c{{m}^{3}}$.
Đáp án C.