Câu hỏi: Trong không gian với hệ tọa độ
A.
B.
C.
D.
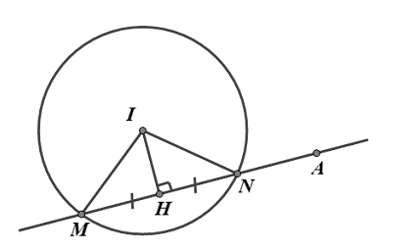 Mặt cầu
Mặt cầu
Ta có
Ta lại có
Mà
Do đó
Do đó
Dấu
A.
B.
C.
D.
Ta có
Ta lại có
Mà
Do đó
Do đó
Dấu
Đáp án D.