Google
Câu hỏi: Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng $d:\dfrac{x-1}{2}=\dfrac{y-2}{1}=\dfrac{z+1}{3}$ và mặt phẳng $\left( P \right):x+y+z-3=0$. Đường thẳng ${d}'$ là hình chiếu của $d$ theo phương $Ox$ lên $\left( P \right)$ ; ${d}'$ nhận $\overrightarrow{u}\left( a;b;2019 \right)$ làm một vectơ chỉ phương. Xác định tổng $a+b$
A. $2019$.
B. $-2019$.
C. $2018$.
D. $-2020$.
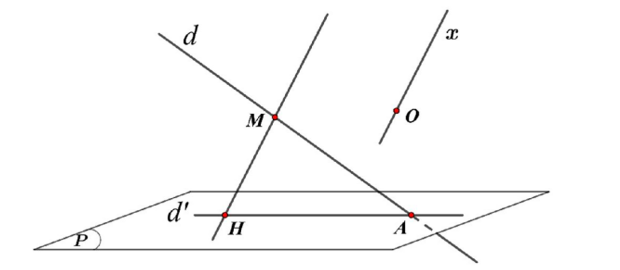Mặt phẳng $\left( P \right)$ có vecto pháp tuyến $\overrightarrow{{{n}_{\left( P \right)}}}=\left( 1;1;1 \right)$.
Đường thẳng $d$ có vecto chỉ phương $\overrightarrow{{{u}_{d}}}=\left( 2;1;3 \right)$, đường thẳng chứa trục $Ox$ có vecto chỉ phương $\overrightarrow{i}=\left( 1;0;0 \right)$.
Gọi $\left( Q \right)$ là mặt phẳng chứa đường thẳng $d$ và song song ( hoặc chứa) trục $Ox$.
Khi đó $\left( Q \right)$ có vecto pháp tuyến $\overrightarrow{{{n}_{\left( Q \right)}}}=\left[ \overrightarrow{{{u}_{d}}};\overrightarrow{i} \right]=\left( 0;3;-1 \right)$.
Ta có ${d}'=\left( P \right)\cap \left( Q \right)$ $\Rightarrow \overrightarrow{{{u}_{{{d}'}}}}=\left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{n{_{\left( Q \right)}}} \right]=\left( -4;1;3 \right)$
Do đó $\overrightarrow{u}=\left( -2692;673;2019 \right)$ cũng là vecto chỉ phương của ${d}'$.
Ta có: $a+b=-2692+673=-2019$.
A. $2019$.
B. $-2019$.
C. $2018$.
D. $-2020$.
Đường thẳng $d$ có vecto chỉ phương $\overrightarrow{{{u}_{d}}}=\left( 2;1;3 \right)$, đường thẳng chứa trục $Ox$ có vecto chỉ phương $\overrightarrow{i}=\left( 1;0;0 \right)$.
Gọi $\left( Q \right)$ là mặt phẳng chứa đường thẳng $d$ và song song ( hoặc chứa) trục $Ox$.
Khi đó $\left( Q \right)$ có vecto pháp tuyến $\overrightarrow{{{n}_{\left( Q \right)}}}=\left[ \overrightarrow{{{u}_{d}}};\overrightarrow{i} \right]=\left( 0;3;-1 \right)$.
Ta có ${d}'=\left( P \right)\cap \left( Q \right)$ $\Rightarrow \overrightarrow{{{u}_{{{d}'}}}}=\left[ \overrightarrow{{{n}_{\left( P \right)}}};\overrightarrow{n{_{\left( Q \right)}}} \right]=\left( -4;1;3 \right)$
Do đó $\overrightarrow{u}=\left( -2692;673;2019 \right)$ cũng là vecto chỉ phương của ${d}'$.
Ta có: $a+b=-2692+673=-2019$.
Đáp án B.