Câu hỏi: Trong không gian $Oxyz$, xét mặt cầu $\left( S \right)$ có tâm $I\left( 4; 8; 12 \right)$ và bán kính $R$ thay đổi. Có bao nhiêu giá trị nguyên của $R$ sao cho ứng với mỗi giá trị đó, tồn tại hai tiếp tuyến của $\left( S \right)$ trong mặt phẳng $\left( Oyz \right)$ mà hai tiếp tuyến đó cùng đi qua $O$ và góc giữa chúng không nhỏ hơn $60{}^\circ $ ?
A. $6$.
B. $2$.
C. $10$.
D. $5$.
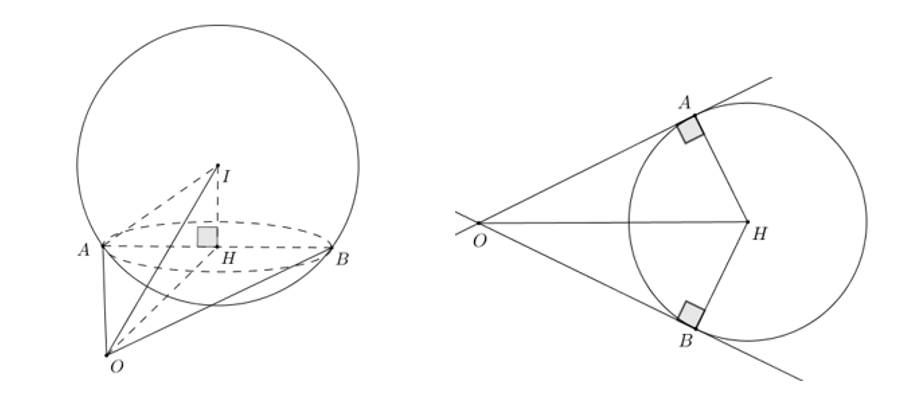
Giả sử 2 tiếp tuyến $OA,OB$, theo giả thiết suy ra $\left( \overrightarrow{OA}, \overrightarrow{OB} \right)\ge 60{}^\circ $. Suy ra $30{}^\circ \le \widehat{AOH}\le 60{}^\circ $
Gọi $H$ là hình chiếu của $I$ trên $\left( Oyz \right)$, suy ra $H\left( 0; 8; 12 \right)$, suy ra $OH=4\sqrt{13}$
Xét tam giác $OAH$ có: $HA=OH\sin \widehat{AOH}\ge 4\sqrt{13}\sin 30{}^\circ =2\sqrt{13}$
Ta có $2\sqrt{13}\le HA<2\sqrt{39}$ $\Rightarrow 52\le A{{H}^{2}}\le 156$
$\Rightarrow 52+16\le A{{H}^{2}}+I{{H}^{2}}\le 156+16$
$\Rightarrow 68\le I{{A}^{2}}\le 172\Rightarrow 68\le {{R}^{2}}\le 172$ hay $8,24\le R\le 13,11$.
Do $R$ là số nguyên $\Rightarrow R\in \left\{ 9; 10; ...; 13 \right\}$.
Vậy có tất cả 5 giá trị của $R$.
A. $6$.
B. $2$.
C. $10$.
D. $5$.
Giả sử 2 tiếp tuyến $OA,OB$, theo giả thiết suy ra $\left( \overrightarrow{OA}, \overrightarrow{OB} \right)\ge 60{}^\circ $. Suy ra $30{}^\circ \le \widehat{AOH}\le 60{}^\circ $
Gọi $H$ là hình chiếu của $I$ trên $\left( Oyz \right)$, suy ra $H\left( 0; 8; 12 \right)$, suy ra $OH=4\sqrt{13}$
Xét tam giác $OAH$ có: $HA=OH\sin \widehat{AOH}\ge 4\sqrt{13}\sin 30{}^\circ =2\sqrt{13}$
Ta có $2\sqrt{13}\le HA<2\sqrt{39}$ $\Rightarrow 52\le A{{H}^{2}}\le 156$
$\Rightarrow 52+16\le A{{H}^{2}}+I{{H}^{2}}\le 156+16$
$\Rightarrow 68\le I{{A}^{2}}\le 172\Rightarrow 68\le {{R}^{2}}\le 172$ hay $8,24\le R\le 13,11$.
Do $R$ là số nguyên $\Rightarrow R\in \left\{ 9; 10; ...; 13 \right\}$.
Vậy có tất cả 5 giá trị của $R$.
Đáp án D.