Google
Câu hỏi: Trong không gian $Oxyz$, mặt cầu tâm $I\left( 1;2;-1 \right)$ cắt mặt phẳng $\left( P \right): 2x-y+2z-1=0$ theo giao tuyến là một đường tròn có bán kính bằng $2\sqrt{2}$ có phương trình là
A. ${{\left( x+1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=9$.
B. ${{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=9$.
C. ${{\left( x+1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=3$.
D. ${{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=3$.
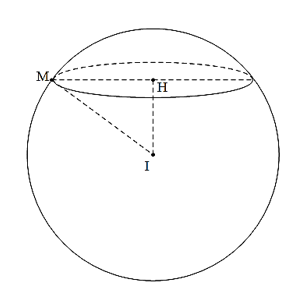Giả sử đường tròn giao tuyến của mặt phẳng $\left( P \right)$ và mặt cầu $\left( S \right)$ có tâm $H$, bán kính $HM$.
$IH=d\left( I,\left( P \right) \right)$ $=\dfrac{\left| 2-2-2-1 \right|}{\sqrt{{{2}^{2}}+{{\left( -1 \right)}^{2}}+{{2}^{2}}}}=1$.
Bán kính của mặt cầu $\left( S \right)$ là $r=IM$ $=\sqrt{{{1}^{2}}+{{\left( 2\sqrt{2} \right)}^{2}}}=3$.
Vậy phương trình của mặt cầu $\left( S \right)$ : ${{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=9$.
A. ${{\left( x+1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=9$.
B. ${{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=9$.
C. ${{\left( x+1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=3$.
D. ${{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=3$.
$IH=d\left( I,\left( P \right) \right)$ $=\dfrac{\left| 2-2-2-1 \right|}{\sqrt{{{2}^{2}}+{{\left( -1 \right)}^{2}}+{{2}^{2}}}}=1$.
Bán kính của mặt cầu $\left( S \right)$ là $r=IM$ $=\sqrt{{{1}^{2}}+{{\left( 2\sqrt{2} \right)}^{2}}}=3$.
Vậy phương trình của mặt cầu $\left( S \right)$ : ${{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+1 \right)}^{2}}=9$.
Đáp án B.