Google
Câu hỏi: Trong không gian $Oxyz$, cho tam giác $ABC$ có $A\left( 1;2;2 \right)$, $B\left( 3;2;0 \right)$ và đường phân giác đỉnh $B$ là $d:\dfrac{x-3}{2}=\dfrac{y-2}{-1}=\dfrac{z}{-1}$. Điểm nào dưới đây thuộc đường thẳng $BC$ ?
A. ${{M}_{3}}\left( 2;3;0 \right)$.
B. ${{M}_{2}}\left( 1;1;0 \right)$.
C. ${{M}_{4}}\left( 1;0;0 \right)$.
D. ${{M}_{1}}\left( 1;5;0 \right)$.
A. ${{M}_{3}}\left( 2;3;0 \right)$.
B. ${{M}_{2}}\left( 1;1;0 \right)$.
C. ${{M}_{4}}\left( 1;0;0 \right)$.
D. ${{M}_{1}}\left( 1;5;0 \right)$.
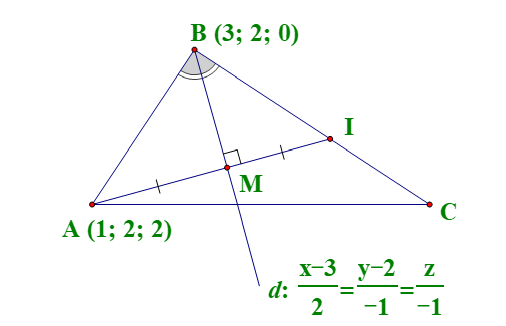
Gọi $I$ là điểm đối xứng của $A$ qua phân giác đỉnh $B$, khi đó $I\in BC$.
Gọi $M$ là giao điểm của $AI$ và phân giác đó suy ra $M$ là trung điểm cạnh $AI$.
Ta có $M\left( 3+2t;2-t;-t \right)$ với $t\in \mathbb{R}$ nên $\overrightarrow{AM}=\left( 2+2t;-t;-2-t \right)$ ; đường thẳng $d$ có véctơ chỉ phương $\overrightarrow{{{u}_{d}}}=\left( 2;-1;-1 \right)$.
Khi đó: $\overrightarrow{AM}.\overrightarrow{{{u}_{d}}}=2.\left( 2+2t \right)+\left( -1 \right).\left( -t \right)+\left( -1 \right).\left( -2-t \right)=0\Leftrightarrow t=-1$ suy ra $M\left( 1;3;1 \right)$.
Lại có $M$ là trung điểm $AI$ nên $\left\{ \begin{aligned}
& {{x}_{I}}=2{{x}_{M}}-{{x}_{A}}=1 \\
& {{y}_{I}}=2{{y}_{M}}-{{y}_{A}}=4 \\
& {{z}_{I}}=2{{z}_{M}}-{{z}_{A}}=0 \\
\end{aligned} \right. $ nên $ I\left( 1;4;0 \right)$.
Ta có: $\overrightarrow{BI}=\left( -2;2;0 \right)$, đường thẳng $BC:\left\{ \begin{aligned}
& \text{qua }B\left( 3;2;0 \right) \\
& \text{c }\!\!\acute{\mathrm{o}}\!\! \text{VTCP} \overrightarrow{u}=\left( -1;1;0 \right) \\
\end{aligned} \right. $ do đó: $ BC:\left\{ \begin{aligned}
& x=3-t \\
& y=2+t \\
& z=0 \\
\end{aligned} \right.$.
Gọi $M$ là giao điểm của $AI$ và phân giác đó suy ra $M$ là trung điểm cạnh $AI$.
Khi đó: $\overrightarrow{AM}.\overrightarrow{{{u}_{d}}}=2.\left( 2+2t \right)+\left( -1 \right).\left( -t \right)+\left( -1 \right).\left( -2-t \right)=0\Leftrightarrow t=-1$ suy ra $M\left( 1;3;1 \right)$.
Lại có $M$ là trung điểm $AI$ nên $\left\{ \begin{aligned}
& {{x}_{I}}=2{{x}_{M}}-{{x}_{A}}=1 \\
& {{y}_{I}}=2{{y}_{M}}-{{y}_{A}}=4 \\
& {{z}_{I}}=2{{z}_{M}}-{{z}_{A}}=0 \\
\end{aligned} \right. $ nên $ I\left( 1;4;0 \right)$.
Ta có: $\overrightarrow{BI}=\left( -2;2;0 \right)$, đường thẳng $BC:\left\{ \begin{aligned}
& \text{qua }B\left( 3;2;0 \right) \\
& \text{c }\!\!\acute{\mathrm{o}}\!\! \text{VTCP} \overrightarrow{u}=\left( -1;1;0 \right) \\
\end{aligned} \right. $ do đó: $ BC:\left\{ \begin{aligned}
& x=3-t \\
& y=2+t \\
& z=0 \\
\end{aligned} \right.$.
Nhận thấy ${{M}_{3}}\in BC$ nên chọn đáp ánA.
Đáp án A.