Trong không gian $Oxyz,$ cho tam giác $ABC$ có $A(3; 4; 4),$...

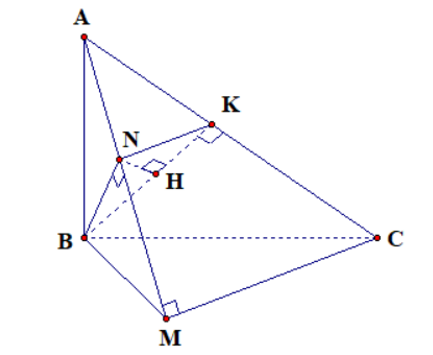Ta có $\overrightarrow{BA}(2; 2; 1),\overrightarrow{BC}(4; -2; -4)\Rightarrow \overrightarrow{BA}.\overrightarrow{BC}=0$ do đó $\Delta ABC$ vuông tại $B$.
$\Rightarrow $ $BA=3;BC=6$.
Từ giả thiết suy ra $\left\{ \begin{aligned}
& AB\bot BC \\
& AB\bot BM \\
\end{aligned} \right.\Rightarrow AB\bot (MBC)$.
Gọi K là hình chiếu của $B$ lên $AC$ nên $(BKN)\bot AC$ cố định.
Xét $\Delta ABC$ vuông tại $B$ có đường cao BK:
$\dfrac{1}{B{{K}^{2}}}=\dfrac{1}{B{{A}^{2}}}+\dfrac{1}{B{{C}^{2}}}=\dfrac{1}{{{3}^{2}}}+\dfrac{1}{{{6}^{2}}}=\dfrac{5}{36}\Rightarrow $ $BK=\dfrac{6\sqrt{5}}{5}$
Ta có $\left\{ \begin{aligned}
& BN\bot AM \\
& BN\bot AC \\
\end{aligned} \right.\Rightarrow $ $ BN\bot \left( AMC \right)\Rightarrow BN\bot NK $ suy ra $ N $ chạy trên đường tròn đường kính $ BK=\dfrac{6\sqrt{5}}{5}$.
Trong $\left( BNK \right)$ kẻ $NH\bot BK\Rightarrow NH\bot \left( ABC \right)\Rightarrow NH=d\left( N,\left( ABC \right) \right)$
Trong tam giác vuông $BNK$ có $NH\le \dfrac{1}{2}BK=\dfrac{3\sqrt{5}}{5}$.
Phương trình mặt phẳng $(BCM)$ đi qua $B$ và có vecto pháp tuyến $\overrightarrow{BA}\left( 2; 2; 1 \right)$ có dạng:
$2x+2y+z-9=0$
Tam giác $BNK$ vuông cân tại $N$ nên $BN=\dfrac{3\sqrt{2}}{\sqrt{5}}$
Xét $\Delta ABM$ vuông tại $B$ có đường cao $BN$ :
$\dfrac{1}{B{{M}^{2}}}=\dfrac{1}{B{{N}^{2}}}-\dfrac{1}{B{{A}^{2}}}=\dfrac{5}{18}-\dfrac{1}{{{3}^{2}}}=\dfrac{1}{6}\Rightarrow $ $BM=\sqrt{6}$
Gọi $M\left( a;b;c \right)$, ta có $\left\{ \begin{aligned}
& BM=\sqrt{6} \\
& \overrightarrow{AM}.\overrightarrow{CM}=0 \\
& M\in \left( BCM \right) \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& {{\left( a-1 \right)}^{2}}+{{\left( b-2 \right)}^{2}}+{{\left( c-3 \right)}^{2}}=6 \\
& \left( a-3 \right)\left( a-5 \right)+\left( b-4 \right)b+\left( c-4 \right)\left( c+1 \right)=0 \\
& 2a+2b+c-9=0 \\
\end{aligned} \right.$
$\Leftrightarrow \left\{ \begin{aligned}
& {{a}^{2}}+{{b}^{2}}+{{c}^{2}}-2a-4b-6c+8=0 \\
& {{a}^{2}}+{{b}^{2}}+{{c}^{2}}-8a-4b-3c+11=0 \\
& 2a+2b+c-9=0 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& {{\left( a-1 \right)}^{2}}+{{\left( b-2 \right)}^{2}}+{{\left( c-3 \right)}^{2}}=6 \\
& 2a-c-1=0 \\
& 2a+2b+c-9=0 \\
\end{aligned} \right.$
$\Leftrightarrow \left\{ \begin{aligned}
& {{\left( a-1 \right)}^{2}}+{{\left( b-2 \right)}^{2}}+{{\left( c-3 \right)}^{2}}=6 \\
& c=2a-1 \\
& b=5-2a \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& 9{{a}^{2}}-30a+20=0 \\
& c=2a-1 \\
& b=5-2a \\
\end{aligned} \right. $ $ \Leftrightarrow \left\{ \begin{aligned}
& a=\dfrac{5+\sqrt{5}}{3} \\
& b=\dfrac{5+2\sqrt{5}}{3} \\
& c=\dfrac{7+2\sqrt{5}}{3} \\
\end{aligned} \right.\vee \Leftrightarrow \left\{ \begin{aligned}
& a=\dfrac{5-\sqrt{5}}{3} \\
& b=\dfrac{5-2\sqrt{5}}{3} \\
& c=\dfrac{7-2\sqrt{5}}{3} \\
\end{aligned} \right.$.
Vậy khoảng cách từ $N$ đến $(ABC)$ có giá trị lớn nhất bằng $\dfrac{3\sqrt{5}}{5}$
khi $M\left( a;b;c \right)$ với $a;b;c$ như trên.