Google
Câu hỏi: Trong không gian $Oxyz$, cho mặt phẳng $\left( P \right):8x-4y+3z-12=0$ và hai điểm $A\left( -2;-2;\dfrac{5}{2} \right)$, $B\left( 2;-4;-\dfrac{5}{2} \right)$. Mặt phẳng $\left( Q \right)$ chứa đường thẳng $AB$ và tạo với $\left( P \right)$ một góc nhỏ nhất. Khoảng cách từ gốc toạ độ $O$ đến mặt phẳng $\left( Q \right)$ bằng.
A. $\sqrt{3}$.
B. $1$
C. $2$.
D. $\sqrt{2}$.
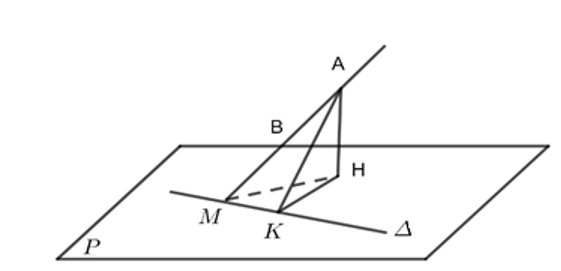Gọi $\left( \Delta \right)$ là giao tuyến của hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$.
$H$ là hình chiếu vuông góc của $A$ trên mặt phẳng $\left( P \right)$, $K$ là hình chiếu vuông góc của $H$ trên đường thẳng $\left( \Delta \right)$. Suy ra $AK$ và $HK$ cùng vuông góc $\left( \Delta \right)$. Hay góc giữa mặt phẳng $\left( P \right)$ và $\left( Q \right)$ là $\widehat{AKH}$.
Đề nhỏ nhất thì $HK$ nhỏ nhất.
Mặt khác $HK\le HM$. Dấu $''=''$ xảy ra khi $HK=HM$ hay $K\equiv M$.
Khi đó góc giữa $\left( P \right)$ và $\left( Q \right)$ nhỏ nhất khi và chỉ khi $\Delta \bot AB$.
Ta có $\left( P \right)$ có véctơ pháp tuyến $\overrightarrow{n}=\left( 8;-4;3 \right)$ và $\overrightarrow{AB}=\left( 4;-2;-5 \right)$. Suy ra véctơ chỉ phương của đường thẳng $\left( \Delta \right)$ là: $\overrightarrow{{{u}_{\Delta }}}=\left( 1;2;0 \right)$.
Suy ra vectơ pháp tuyến của mặt phẳng $\left( Q \right)$ là $\overrightarrow{{{n}_{Q}}}=\left[ \overrightarrow{AB},\overrightarrow{{{u}_{\Delta }}} \right]=5\left( 2;-1;2 \right)$.
Phương trình mặt phẳng $\left( Q \right)$ là: $2x-y+2z-3=0$.
Vậy $d\left( O,\left( Q \right) \right)=1.$
A. $\sqrt{3}$.
B. $1$
C. $2$.
D. $\sqrt{2}$.
$H$ là hình chiếu vuông góc của $A$ trên mặt phẳng $\left( P \right)$, $K$ là hình chiếu vuông góc của $H$ trên đường thẳng $\left( \Delta \right)$. Suy ra $AK$ và $HK$ cùng vuông góc $\left( \Delta \right)$. Hay góc giữa mặt phẳng $\left( P \right)$ và $\left( Q \right)$ là $\widehat{AKH}$.
Đề nhỏ nhất thì $HK$ nhỏ nhất.
Mặt khác $HK\le HM$. Dấu $''=''$ xảy ra khi $HK=HM$ hay $K\equiv M$.
Khi đó góc giữa $\left( P \right)$ và $\left( Q \right)$ nhỏ nhất khi và chỉ khi $\Delta \bot AB$.
Ta có $\left( P \right)$ có véctơ pháp tuyến $\overrightarrow{n}=\left( 8;-4;3 \right)$ và $\overrightarrow{AB}=\left( 4;-2;-5 \right)$. Suy ra véctơ chỉ phương của đường thẳng $\left( \Delta \right)$ là: $\overrightarrow{{{u}_{\Delta }}}=\left( 1;2;0 \right)$.
Suy ra vectơ pháp tuyến của mặt phẳng $\left( Q \right)$ là $\overrightarrow{{{n}_{Q}}}=\left[ \overrightarrow{AB},\overrightarrow{{{u}_{\Delta }}} \right]=5\left( 2;-1;2 \right)$.
Phương trình mặt phẳng $\left( Q \right)$ là: $2x-y+2z-3=0$.
Vậy $d\left( O,\left( Q \right) \right)=1.$
Đáp án B.