Google
Câu hỏi: Trong không gian $Oxyz$, cho mặt phẳng $\left( P \right):x+y-2z+10=0$ và hai điểm $A\left( 1;-1;2 \right)$, $B\left( 2;0;-4 \right)$. Gọi $M\left( a;b;c \right)$ là điểm thuộc đoạn $AB$ sao cho luôn tồn tại hai mặt cầu có bán kính $R=\sqrt{6}$ tiếp xúc mặt phẳng $\left( P \right)$, đồng thời tiếp xúc với đoạn $AB$ tại $M$. Gọi $T=\left[ m;n \right)$ là tập giá trị của biểu thức $25{{a}^{2}}+{{b}^{2}}+2{{c}^{2}}$. Khi đó $m.n$ bằng
A. $\dfrac{1340}{19}$
B. $140$.
C. $\dfrac{23596}{19}$.
D. $86$.
A. $\dfrac{1340}{19}$
B. $140$.
C. $\dfrac{23596}{19}$.
D. $86$.
Ta có: $\overrightarrow{AB}=\left( 1 ;1 ;-6 \right)$, nên phương trình đường thẳng $AB$ là: $\left\{ \begin{aligned}
& x=1+t \\
& y=-1+t \\
& z=2-6t \\
\end{aligned} \right.$.
Mặt khác, hai điểm $A$ và $B$ cùng phía với mặt phẳng $\left( P \right)$. Gọi $\left( Q \right)$ là mặt phẳng song song với $\left( P \right)$ sao cho $d\left( \left( P \right) ,\left( Q \right) \right)=\sqrt{6}$ ở vị trí như hình vẽ.
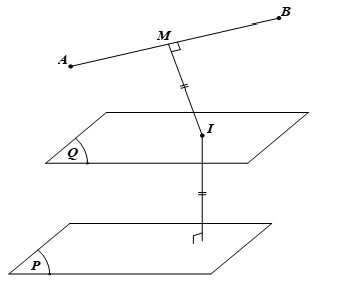Khi đó, phương trình mặt phẳng $\left( Q \right)$ là: $x+y-2z+4=0$.
Ta có: $M$ thuộc đoạn thẳng $AB$, suy ra $M\left( 1+t ;-1+t ;2-6t \right)$, với $t\in \left[ 0 ;1 \right] \left( * \right)$.
Gọi $I\left( x ;y ;z \right)$ là tâm của mặt cầu thoả mãn yêu cầu bài toán, khi đó:$\left\{ \begin{aligned}
& I\in \left( Q \right) \\
& \overrightarrow{IM}\bot \overrightarrow{AB} \\
& IM=\sqrt{6} \\
\end{aligned} \right. $ $ \Leftrightarrow \left\{ \begin{aligned}
& x+y-2z+4=0 \\
& 1\left( 1+t-x \right)+1\left( -1+t-y \right)-6\left( 2-6t-z \right)=0 \\
& {{\left( 1+t-x \right)}^{2}}+{{\left( -1+t-y \right)}^{2}}+{{\left( 2-6t-z \right)}^{2}}=6 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& x+y+19t=0 \\
& z=\dfrac{-19t+4}{2}\left( 1 \right) \\
& {{\left( x-1-t \right)}^{2}}+{{\left( y+1-t \right)}^{2}}=\dfrac{24-49{{t}^{2}}}{4}\left( 2 \right) \\
\end{aligned} \right.$.
Tồn tại hai mặt cầu thoả mãn yêu cầu bài toán $\Leftrightarrow $ Hệ $\left( 1 \right)$ và $\left( 2 \right)$ có hai nghiệm phân biệt
$\Leftrightarrow \left\{ \begin{aligned}
& 24-49{{t}^{{}}}>0 \\
& \dfrac{\left| 1+t-1+t+19t \right|}{\sqrt{2}}<\sqrt{\dfrac{24-49{{t}^{2}}}{4}} \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& 24-49{{t}^{2}}>0 \\
& {{t}^{2}}<\dfrac{24}{931} \\
\end{aligned} \right.\Leftrightarrow -\sqrt{\dfrac{24}{931}}<t<\sqrt{\dfrac{24}{931}}$.
Giao với $\left( * \right)$, ta được: $t\in \left[ 0 ;\sqrt{\dfrac{24}{931}} \right)$.
Ta có: $25{{a}^{2}}+{{b}^{2}}+2{{c}^{2}}=25{{\left( 1+t \right)}^{2}}+{{\left( -1+t \right)}^{2}}+2{{\left( 2-6t \right)}^{2}}=98{{t}^{2}}+34$.
Xét hàm số $f\left( t \right)=98{{t}^{2}}+34$ trên $\left[ 0 ;\sqrt{\dfrac{24}{931}} \right)$, có ${f}'\left( t \right)=196t>0, \forall t\in \left[ 0 ;\sqrt{\dfrac{24}{931}} \right)$.
Suy ra: tập giá trị $T=\left[ f\left( 0 \right) ;f\left( \sqrt{\dfrac{24}{931}} \right) \right)\Rightarrow T=\left[ 34 ;\dfrac{694}{19} \right)\Rightarrow m=34, n=\dfrac{694}{19}$.
Vậy $m+n=\dfrac{1340}{19}$.
& x=1+t \\
& y=-1+t \\
& z=2-6t \\
\end{aligned} \right.$.
Mặt khác, hai điểm $A$ và $B$ cùng phía với mặt phẳng $\left( P \right)$. Gọi $\left( Q \right)$ là mặt phẳng song song với $\left( P \right)$ sao cho $d\left( \left( P \right) ,\left( Q \right) \right)=\sqrt{6}$ ở vị trí như hình vẽ.
Ta có: $M$ thuộc đoạn thẳng $AB$, suy ra $M\left( 1+t ;-1+t ;2-6t \right)$, với $t\in \left[ 0 ;1 \right] \left( * \right)$.
Gọi $I\left( x ;y ;z \right)$ là tâm của mặt cầu thoả mãn yêu cầu bài toán, khi đó:$\left\{ \begin{aligned}
& I\in \left( Q \right) \\
& \overrightarrow{IM}\bot \overrightarrow{AB} \\
& IM=\sqrt{6} \\
\end{aligned} \right. $ $ \Leftrightarrow \left\{ \begin{aligned}
& x+y-2z+4=0 \\
& 1\left( 1+t-x \right)+1\left( -1+t-y \right)-6\left( 2-6t-z \right)=0 \\
& {{\left( 1+t-x \right)}^{2}}+{{\left( -1+t-y \right)}^{2}}+{{\left( 2-6t-z \right)}^{2}}=6 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& x+y+19t=0 \\
& z=\dfrac{-19t+4}{2}\left( 1 \right) \\
& {{\left( x-1-t \right)}^{2}}+{{\left( y+1-t \right)}^{2}}=\dfrac{24-49{{t}^{2}}}{4}\left( 2 \right) \\
\end{aligned} \right.$.
Tồn tại hai mặt cầu thoả mãn yêu cầu bài toán $\Leftrightarrow $ Hệ $\left( 1 \right)$ và $\left( 2 \right)$ có hai nghiệm phân biệt
$\Leftrightarrow \left\{ \begin{aligned}
& 24-49{{t}^{{}}}>0 \\
& \dfrac{\left| 1+t-1+t+19t \right|}{\sqrt{2}}<\sqrt{\dfrac{24-49{{t}^{2}}}{4}} \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& 24-49{{t}^{2}}>0 \\
& {{t}^{2}}<\dfrac{24}{931} \\
\end{aligned} \right.\Leftrightarrow -\sqrt{\dfrac{24}{931}}<t<\sqrt{\dfrac{24}{931}}$.
Giao với $\left( * \right)$, ta được: $t\in \left[ 0 ;\sqrt{\dfrac{24}{931}} \right)$.
Ta có: $25{{a}^{2}}+{{b}^{2}}+2{{c}^{2}}=25{{\left( 1+t \right)}^{2}}+{{\left( -1+t \right)}^{2}}+2{{\left( 2-6t \right)}^{2}}=98{{t}^{2}}+34$.
Xét hàm số $f\left( t \right)=98{{t}^{2}}+34$ trên $\left[ 0 ;\sqrt{\dfrac{24}{931}} \right)$, có ${f}'\left( t \right)=196t>0, \forall t\in \left[ 0 ;\sqrt{\dfrac{24}{931}} \right)$.
Suy ra: tập giá trị $T=\left[ f\left( 0 \right) ;f\left( \sqrt{\dfrac{24}{931}} \right) \right)\Rightarrow T=\left[ 34 ;\dfrac{694}{19} \right)\Rightarrow m=34, n=\dfrac{694}{19}$.
Vậy $m+n=\dfrac{1340}{19}$.
Đáp án C.