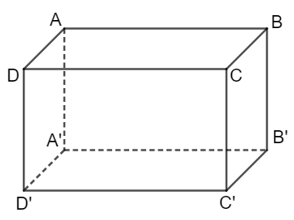
Câu hỏi: Trong không gian $Oxyz$, cho hình hộp $ABCD.{A}'{B}'{C}'{D}'$ có $A(0;0;1),{B}'(1;0;0),{C}'(1;1;0)$. Tìm tọa độ điểm $D$
A. $D(0;-1;1)$.
B. $D(0;1;1)$.
C. $D(1;1;1)$.
D. $D(0;1;0)$.
A. $D(0;-1;1)$.
B. $D(0;1;1)$.
C. $D(1;1;1)$.
D. $D(0;1;0)$.
Ta có : $\overrightarrow{AD}=\overrightarrow{{B}'{C}'}\Leftrightarrow \left\{ \begin{aligned}
& {{x}_{D}}-0=1-1 \\
& {{y}_{D}}-0=1-0 \\
& {{z}_{D}}-1=0-0 \\
\end{aligned} \right.\to \left\{ \begin{aligned}
& {{x}_{D}}=0 \\
& {{y}_{D}}=1 \\
& {{z}_{D}}=1 \\
\end{aligned} \right.$.
Vậy tọa độ điểm $D(0;1;1)$.
& {{x}_{D}}-0=1-1 \\
& {{y}_{D}}-0=1-0 \\
& {{z}_{D}}-1=0-0 \\
\end{aligned} \right.\to \left\{ \begin{aligned}
& {{x}_{D}}=0 \\
& {{y}_{D}}=1 \\
& {{z}_{D}}=1 \\
\end{aligned} \right.$.
Vậy tọa độ điểm $D(0;1;1)$.
Đáp án B.