Câu hỏi: Trong đợt hội trại được tổ chức tại trường THPT Nguyễn Tất Thành, Đoàn trường có thể thực hiện một dự án ảnh trưng bày trên một pano có dạng parabol như hình vẽ. Biết rằng đoàn trường sẽ yêu cầu các lớp gửi hình dự thi và dán lên khu vực hình chữ nhật ABCD, phần còn lại sẽ được trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000 đồng cho một ${{m}^{2}}$ bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm tròn đến hàng nghìn)?

A. 1.230.000.
B. 902.000.
C. 900.000.
D. 1.232.000.
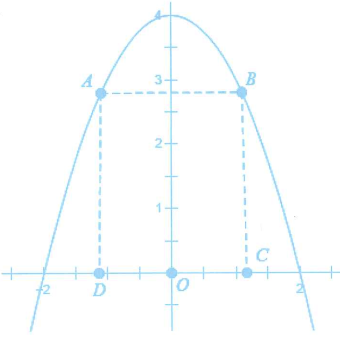
Ta có hình trên cao 4, rộng 4 nến biểu diễn qua một Parabol $y=-{{x}^{2}}+4$.
Chi phí thấp nhất nếu diện tích hình chữ nhật lớn nhất.
Gọi $C\left( x;0 \right)$ với $0<x<2$ thì suy ra $B\left( x;-{{x}^{2}}+4 \right)$
Diện tích hình chữ nhật là
$S\left( x \right)=2\left| x\left( -{{x}^{2}}+4 \right) \right|=2\left( -{{x}^{3}}+4x \right)$ ;
${S}'\left( x \right)=2\left( -3{{x}^{2}}+4 \right)=0\Leftrightarrow x=\dfrac{2\sqrt{3}}{3}$
Dễ thấy ${{S}_{\max }}=S\left( \dfrac{2\sqrt{3}}{3} \right)=\dfrac{4\sqrt{3}}{3}.\left( 4-\dfrac{4}{3} \right)=\dfrac{32\sqrt{3}}{9}$
Diện tích nhỏ nhất phần hoa văn là
${{X}_{\min }}=\int\limits_{-2}^{2}{\left( 4-{{x}^{2}} \right)dx}-{{S}_{\max }}=\dfrac{32}{3}-\dfrac{32\sqrt{3}}{9}$
Số tiền nhỏ nhất là ${{X}_{\min }}.200000=901.652\approx 902.000$

A. 1.230.000.
B. 902.000.
C. 900.000.
D. 1.232.000.
Ta có hình trên cao 4, rộng 4 nến biểu diễn qua một Parabol $y=-{{x}^{2}}+4$.
Chi phí thấp nhất nếu diện tích hình chữ nhật lớn nhất.
Gọi $C\left( x;0 \right)$ với $0<x<2$ thì suy ra $B\left( x;-{{x}^{2}}+4 \right)$
Diện tích hình chữ nhật là
$S\left( x \right)=2\left| x\left( -{{x}^{2}}+4 \right) \right|=2\left( -{{x}^{3}}+4x \right)$ ;
${S}'\left( x \right)=2\left( -3{{x}^{2}}+4 \right)=0\Leftrightarrow x=\dfrac{2\sqrt{3}}{3}$
Dễ thấy ${{S}_{\max }}=S\left( \dfrac{2\sqrt{3}}{3} \right)=\dfrac{4\sqrt{3}}{3}.\left( 4-\dfrac{4}{3} \right)=\dfrac{32\sqrt{3}}{9}$
Diện tích nhỏ nhất phần hoa văn là
${{X}_{\min }}=\int\limits_{-2}^{2}{\left( 4-{{x}^{2}} \right)dx}-{{S}_{\max }}=\dfrac{32}{3}-\dfrac{32\sqrt{3}}{9}$
Số tiền nhỏ nhất là ${{X}_{\min }}.200000=901.652\approx 902.000$
Đáp án B.