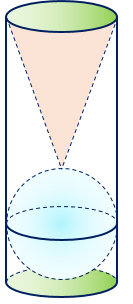
Câu hỏi: Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng của cốcnước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc trànra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày củalớp vỏ thủy tinh).
A. $\dfrac{2}{3}$
B. $\dfrac{5}{9}$
C. $\dfrac{4}{9}$
D. $\dfrac{1}{2}$

A. $\dfrac{2}{3}$
B. $\dfrac{5}{9}$
C. $\dfrac{4}{9}$
D. $\dfrac{1}{2}$
Gọi $r$ là bán kính đáy của cốc nước.
Khi đó:
Chiều cao cốc nước là $h=6r.$ Thể tích lượng nước ban đầu bằng: $V=\pi {{r}^{2}}h=6\pi {{r}^{3}}.$
Viên bi có đường kính bằng đường kính cốc nước nên thể tích bằng ${{V}_{1}}=\dfrac{4}{3}\pi {{r}^{3}}.$
Khối nón có chiều cao bằng $6r-2r=4r$ nên có thể tích bằng ${{V}_{2}}=\dfrac{1}{3}\pi {{r}^{2}}4r=\dfrac{4}{3}\pi {{r}^{3}}$
Cho nên thể tích nước còn lại bằng $V-{{V}_{1}}-{{V}_{2}}=6\pi {{r}^{3}}-\dfrac{4}{3}\pi {{r}^{3}}-\dfrac{4}{3}\pi {{r}^{3}}=\dfrac{10}{3}\pi {{r}^{3}}.$
Suy ra tỉ số giữa số nước còn lại và số nước ban đầu bằng $\dfrac{\dfrac{10}{3}\pi {{r}^{3}}}{6\pi {{r}^{3}}}=\dfrac{5}{9}.$
Vậy ta chọn phương án B.
Khi đó:
Chiều cao cốc nước là $h=6r.$ Thể tích lượng nước ban đầu bằng: $V=\pi {{r}^{2}}h=6\pi {{r}^{3}}.$
Viên bi có đường kính bằng đường kính cốc nước nên thể tích bằng ${{V}_{1}}=\dfrac{4}{3}\pi {{r}^{3}}.$
Khối nón có chiều cao bằng $6r-2r=4r$ nên có thể tích bằng ${{V}_{2}}=\dfrac{1}{3}\pi {{r}^{2}}4r=\dfrac{4}{3}\pi {{r}^{3}}$
Cho nên thể tích nước còn lại bằng $V-{{V}_{1}}-{{V}_{2}}=6\pi {{r}^{3}}-\dfrac{4}{3}\pi {{r}^{3}}-\dfrac{4}{3}\pi {{r}^{3}}=\dfrac{10}{3}\pi {{r}^{3}}.$
Suy ra tỉ số giữa số nước còn lại và số nước ban đầu bằng $\dfrac{\dfrac{10}{3}\pi {{r}^{3}}}{6\pi {{r}^{3}}}=\dfrac{5}{9}.$
Vậy ta chọn phương án B.
Đáp án B.