Thể tích khối tròn xoay tạo thành khi quay quanh trục hoành hình...

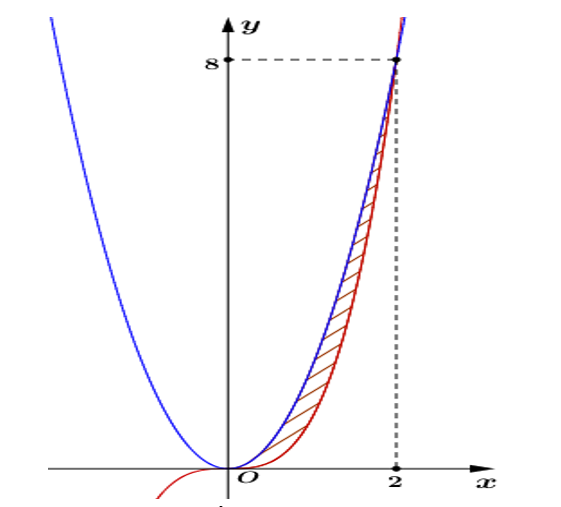Hoành độ giao điểm của đường $y={{x}^{3}}$ với $y=2{{x}^{2}}$ là $x=0; x=2$. Vậy thể tích của khối tròn xoay cần tính là: $V=\pi \int\limits_{0}^{2}{{{\left( 2{{x}^{2}} \right)}^{2}}dx}-\pi \int\limits_{0}^{2}{{{\left( {{x}^{3}} \right)}^{2}}dx}=\dfrac{256\pi }{35}$.