Google
Anh đang liên hệ nhờ họ thiết kế rồi cho mẫu e ạ :D
Test công thức toán
- Thread starter Tăng Hải Tuân
- Ngày gửi
kiemro721119 Chắc là làm áo ngắn tay
Vâng, xong anh cho mọi xem, đăng kí và chuyển khoản luôn để làm áo :3
Ok em :D
Bá chưa :D
Dạng ảnh :
Cho x,y,z là các số thực không âm thay đổi thỏa mãn:
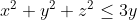
Tìm min:
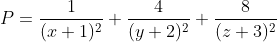
Ta có:
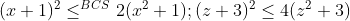
Suy ra có:
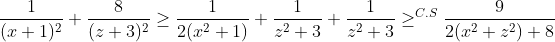
Theo bài:
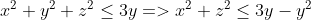
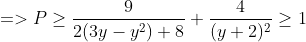Vậy
Kết quả trả về : \left(Đã được đổi hết từ ảnh thành mã latex\right)
Cho x, y, z là các số thực không âm thay đổi thỏa mãn: $\ x^2+y^2+z^2 \le 3y$.
Tìm min: $\ P=\dfrac{1}{\left(x+1\right)^2}+\dfrac{4}{\left(y+2\right)^2}+\dfrac{8}{\left(z+3\right)^2}$
Ta có:
$\ \left(x+1\right)^2\le^{BCS} 2\left(x^2+1\right);\left(z+3\right)^2\le 4\left(z^2+3\right)$
Suy ra có:
$\ \dfrac{1}{\left(x+1\right)^2}+\dfrac{8}{\left(z+3\right)^2}\ge \dfrac{1}{2\left(x^2+1\right)}+\dfrac{1}{z^2+3}+\dfrac{1}{z^2+3}\ge^{C. S} \dfrac{9}{2\left(x^2+z^2\right)+8}$
Theo bài: $\ x^2+y^2+z^2\le 3y\Rightarrow x^2+z^2\le 3y-y^2$
$\ \Rightarrow P\ge\dfrac{9}{2\left(3y-y^2\right)+8}+\dfrac{4}{\left(y+2\right)^2}\ge 1$
$\ \Leftrightarrow \left(y-2\right)^2\left(2y^2+10y+9\right)\ge 0 \Rightarrow TRUE$
Vậy $\ P_{Min}=1\Leftrightarrow \left(x;y;z\right)=\left(1;2;1\right)$
Cho x,y,z là các số thực không âm thay đổi thỏa mãn:
Tìm min:
Ta có:
Suy ra có:
Theo bài:
Kết quả trả về : \left(Đã được đổi hết từ ảnh thành mã latex\right)
Cho x, y, z là các số thực không âm thay đổi thỏa mãn: $\ x^2+y^2+z^2 \le 3y$.
Tìm min: $\ P=\dfrac{1}{\left(x+1\right)^2}+\dfrac{4}{\left(y+2\right)^2}+\dfrac{8}{\left(z+3\right)^2}$
Ta có:
$\ \left(x+1\right)^2\le^{BCS} 2\left(x^2+1\right);\left(z+3\right)^2\le 4\left(z^2+3\right)$
Suy ra có:
$\ \dfrac{1}{\left(x+1\right)^2}+\dfrac{8}{\left(z+3\right)^2}\ge \dfrac{1}{2\left(x^2+1\right)}+\dfrac{1}{z^2+3}+\dfrac{1}{z^2+3}\ge^{C. S} \dfrac{9}{2\left(x^2+z^2\right)+8}$
Theo bài: $\ x^2+y^2+z^2\le 3y\Rightarrow x^2+z^2\le 3y-y^2$
$\ \Rightarrow P\ge\dfrac{9}{2\left(3y-y^2\right)+8}+\dfrac{4}{\left(y+2\right)^2}\ge 1$
$\ \Leftrightarrow \left(y-2\right)^2\left(2y^2+10y+9\right)\ge 0 \Rightarrow TRUE$
Vậy $\ P_{Min}=1\Leftrightarrow \left(x;y;z\right)=\left(1;2;1\right)$
Nắng
Anh sẽ vì em làm cha thằng bé
Em phát hiện ra trong ảnh copy nó có sẵn code http://latex.codecogs.com :))
Khoảng trắng nó sẽ biến thành: %20
Ví dụ : http://latex.codecogs.com/gif.latex?x\sqrt{1-y^2} y\sqrt{1-x^2}
Và mình phải xử lí nó :3.
Ngoài ra còn 1 số kí tự khác nữa, ví dụ : >, <, "
Cái này do a viết ra :3.
Quá tuyệt anh ạ.