Google
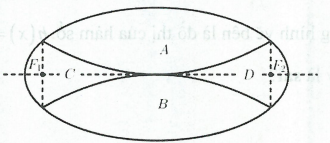
Câu hỏi: Nhà trường dự định làm một vườn hoa dạng elip được chia ra làm bốn phần bởi hai đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ dài trục lớn, trục nhỏ của elip lần lượt là 8m và 4m, gọi ${{F}_{1}}$, ${{F}_{2}}$ là hai tiêu điểm của elip. Phần A, B dùng để trồng hoa, phần C, D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250000 đ và 150000 đ. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn).
A. 5676000 đ.
B. 4766000 đ.
C. 4656000 đ.
D. 5455000 đ.
B. 4766000 đ.
C. 4656000 đ.
D. 5455000 đ.
Gắn hệ trục tọa độ như hình vẽ. Gọi N thuộc cung phần tư thứ nhất là giao điểm của $\left( P \right)$ và $\left( E \right)$.
Do elip có độ dài trục lớn $2a=8\Leftrightarrow a=4$, độ dài trục nhỏ $2b=4\Leftrightarrow b=2$.
Diện tích của $\left( E \right)$ là ${{S}_{\left( E \right)}}=\pi ab=8\pi $.
Phương trình chính tắc $\left( E \right)$ là $\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{4}=1$. Suy ra $y=\pm \dfrac{1}{2}\sqrt{16-{{x}^{2}}}$.
Ta có $c=\sqrt{{{a}^{2}}-{{b}^{2}}}=2\sqrt{3}\Rightarrow {{F}_{2}}\left( 2\sqrt{3};0 \right)$.
Do N và ${{F}_{2}}$ có cùng hoành độ $\Rightarrow N\left( 2\sqrt{3};1 \right)$.
Gọi $\left( P \right)$ : $y=k{{x}^{2}}$ là parabol nằm ở phía trên trục Ox.
Do $N\in \left( P \right)$ ta có $1=k{{\left( 2\sqrt{3} \right)}^{2}}\Leftrightarrow k=\dfrac{1}{12}$. Suy ra $\left( P \right)$ : $y=\dfrac{1}{12}{{x}^{2}}$.
Diện tích phần A là ${{S}_{A}}=\int\limits_{-2\sqrt{3}}^{2\sqrt{3}}{\left( \dfrac{1}{2}\sqrt{16-{{x}^{2}}}-\dfrac{1}{12}{{x}^{2}} \right)dx}=2\int\limits_{0}^{2\sqrt{3}}{\left( \dfrac{1}{2}\sqrt{16-{{x}^{2}}}-\dfrac{1}{12}{{x}^{2}} \right)dx}$
$=\int\limits_{0}^{2\sqrt{3}}{\sqrt{16-{{x}^{2}}}dx}-\dfrac{1}{6}\int\limits_{0}^{2\sqrt{3}}{{{x}^{2}}dx}={{I}_{1}}-{{I}_{2}}$
Xét ${{I}_{1}}=\int\limits_{0}^{2\sqrt{3}}{\sqrt{16-{{x}^{2}}}dx}$. Đặt $x=4\sin t\Rightarrow dx=4\cos tdt$. Đổi cận
Khi đó ${{I}_{1}}=\int\limits_{0}^{\dfrac{\pi }{3}}{\sqrt{16-16{{\sin }^{2}}t}.4\cos tdt}$
$=16\int\limits_{0}^{\dfrac{\pi }{3}}{{{\cos }^{2}}tdt}=8\int\limits_{0}^{\dfrac{\pi }{3}}{\left( 1+\cos 2t \right)dt}=8\left( t+\dfrac{1}{2}\sin 2t \right)\left| \begin{aligned}
& ^{\dfrac{\pi }{3}} \\
& _{0} \\
\end{aligned} \right.=8\left( \dfrac{\pi }{3}+\dfrac{\sqrt{3}}{4} \right)$.
Ta có ${{I}_{2}}=\dfrac{1}{6}\int\limits_{0}^{2\sqrt{3}}{{{x}^{2}}dx}=\dfrac{1}{18}{{x}^{3}}\left| \begin{aligned}
& ^{2\sqrt{3}} \\
& _{0} \\
\end{aligned} \right.=\dfrac{4\sqrt{3}}{3}$
Suy ra ${{S}_{A}}={{I}_{1}}-{{I}_{2}}=\dfrac{8\pi +2\sqrt{3}}{3}\Rightarrow {{S}_{A}}+{{S}_{B}}=2{{S}_{A}}=\dfrac{16\pi +4\sqrt{3}}{3}$.
Tổng diện tích phần C, D là ${{S}_{C}}+{{S}_{D}}={{S}_{\left( E \right)}}-\left( {{S}_{A}}+{{S}_{B}} \right)=\dfrac{8\pi -4\sqrt{3}}{3}$.
Khi đó tổng số tiền để hoàn thành vườn hoa trên là
$\dfrac{16\pi +4\sqrt{3}}{3}.250000+\dfrac{8\pi -4\sqrt{3}}{3}.150000\approx 5676000$ đ.
Diện tích của $\left( E \right)$ là ${{S}_{\left( E \right)}}=\pi ab=8\pi $.
Phương trình chính tắc $\left( E \right)$ là $\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{4}=1$. Suy ra $y=\pm \dfrac{1}{2}\sqrt{16-{{x}^{2}}}$.
Ta có $c=\sqrt{{{a}^{2}}-{{b}^{2}}}=2\sqrt{3}\Rightarrow {{F}_{2}}\left( 2\sqrt{3};0 \right)$.
Do N và ${{F}_{2}}$ có cùng hoành độ $\Rightarrow N\left( 2\sqrt{3};1 \right)$.
Gọi $\left( P \right)$ : $y=k{{x}^{2}}$ là parabol nằm ở phía trên trục Ox.
Do $N\in \left( P \right)$ ta có $1=k{{\left( 2\sqrt{3} \right)}^{2}}\Leftrightarrow k=\dfrac{1}{12}$. Suy ra $\left( P \right)$ : $y=\dfrac{1}{12}{{x}^{2}}$.
Diện tích phần A là ${{S}_{A}}=\int\limits_{-2\sqrt{3}}^{2\sqrt{3}}{\left( \dfrac{1}{2}\sqrt{16-{{x}^{2}}}-\dfrac{1}{12}{{x}^{2}} \right)dx}=2\int\limits_{0}^{2\sqrt{3}}{\left( \dfrac{1}{2}\sqrt{16-{{x}^{2}}}-\dfrac{1}{12}{{x}^{2}} \right)dx}$
$=\int\limits_{0}^{2\sqrt{3}}{\sqrt{16-{{x}^{2}}}dx}-\dfrac{1}{6}\int\limits_{0}^{2\sqrt{3}}{{{x}^{2}}dx}={{I}_{1}}-{{I}_{2}}$
Xét ${{I}_{1}}=\int\limits_{0}^{2\sqrt{3}}{\sqrt{16-{{x}^{2}}}dx}$. Đặt $x=4\sin t\Rightarrow dx=4\cos tdt$. Đổi cận
x | 0 | $2\sqrt{3}$ |
t | 0 | $\dfrac{\pi }{3}$ |
$=16\int\limits_{0}^{\dfrac{\pi }{3}}{{{\cos }^{2}}tdt}=8\int\limits_{0}^{\dfrac{\pi }{3}}{\left( 1+\cos 2t \right)dt}=8\left( t+\dfrac{1}{2}\sin 2t \right)\left| \begin{aligned}
& ^{\dfrac{\pi }{3}} \\
& _{0} \\
\end{aligned} \right.=8\left( \dfrac{\pi }{3}+\dfrac{\sqrt{3}}{4} \right)$.
Ta có ${{I}_{2}}=\dfrac{1}{6}\int\limits_{0}^{2\sqrt{3}}{{{x}^{2}}dx}=\dfrac{1}{18}{{x}^{3}}\left| \begin{aligned}
& ^{2\sqrt{3}} \\
& _{0} \\
\end{aligned} \right.=\dfrac{4\sqrt{3}}{3}$
Suy ra ${{S}_{A}}={{I}_{1}}-{{I}_{2}}=\dfrac{8\pi +2\sqrt{3}}{3}\Rightarrow {{S}_{A}}+{{S}_{B}}=2{{S}_{A}}=\dfrac{16\pi +4\sqrt{3}}{3}$.
Tổng diện tích phần C, D là ${{S}_{C}}+{{S}_{D}}={{S}_{\left( E \right)}}-\left( {{S}_{A}}+{{S}_{B}} \right)=\dfrac{8\pi -4\sqrt{3}}{3}$.
Khi đó tổng số tiền để hoàn thành vườn hoa trên là
$\dfrac{16\pi +4\sqrt{3}}{3}.250000+\dfrac{8\pi -4\sqrt{3}}{3}.150000\approx 5676000$ đ.
Đáp án A.