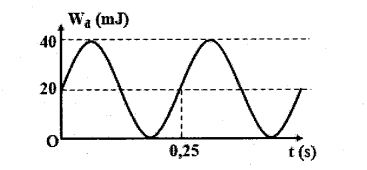
Câu hỏi: Một vật có khối lượng 200g, dao động điều hòa quanh vị trí cân bằng. Đồ thị hình bên mô tả động năng của vật (Wđ )thay đổi phụ thuộc vào thời gian t. Tại t = 0, vật đang có li độ âm. Lấy ${{\pi }^{2}}=10$. Phương trình dao động của vật là
A. $x=5\cos \left( 4\pi t-\dfrac{3\pi }{4} \right)(cm).$
B. $x=4\cos \left( 8\pi t-\dfrac{3\pi }{4} \right)(cm).$
C. $x=4\cos \left( 8\pi t+\dfrac{\pi }{4} \right)(cm).$
D. $x=5\cos \left( 4\pi t+\dfrac{\pi }{4} \right)(cm).$

A. $x=5\cos \left( 4\pi t-\dfrac{3\pi }{4} \right)(cm).$
B. $x=4\cos \left( 8\pi t-\dfrac{3\pi }{4} \right)(cm).$
C. $x=4\cos \left( 8\pi t+\dfrac{\pi }{4} \right)(cm).$
D. $x=5\cos \left( 4\pi t+\dfrac{\pi }{4} \right)(cm).$
HD: Chu kì động năng ${{T}_{d}}=0,25s\Rightarrow T=2{{T}_{d}}=0,5s\Rightarrow \omega =4\pi rad/s$
${{\text{W}}_{\!\!\tilde{\mathrm{n}}\!\!\text{ max}}}=\dfrac{1}{2}m{{\left( \omega A \right)}^{2}}\Leftrightarrow {{40.10}^{-3}}=\dfrac{1}{2}.0,2.{{\left( 4\pi A \right)}^{2}}\Rightarrow A=0,05m=5cm$
Ta có $t=0:{{\text{W}}_{d}}={{\text{W}}_{t}}=\dfrac{\text{W}}{2}\Rightarrow {{x}_{o}}=\pm \dfrac{A\sqrt{2}}{2}$
Mặt khác, ban đầu vật đang có li độ âm và động năng đang tăng nên ${{x}_{o}}=-\dfrac{A\sqrt{2}}{2}$ theo chiều dương
$\Rightarrow \varphi =-\dfrac{3\pi }{4}\Rightarrow x=5\cos \left( 4\pi t-\dfrac{3\pi }{4} \right)(cm).$
${{\text{W}}_{\!\!\tilde{\mathrm{n}}\!\!\text{ max}}}=\dfrac{1}{2}m{{\left( \omega A \right)}^{2}}\Leftrightarrow {{40.10}^{-3}}=\dfrac{1}{2}.0,2.{{\left( 4\pi A \right)}^{2}}\Rightarrow A=0,05m=5cm$
Ta có $t=0:{{\text{W}}_{d}}={{\text{W}}_{t}}=\dfrac{\text{W}}{2}\Rightarrow {{x}_{o}}=\pm \dfrac{A\sqrt{2}}{2}$
Mặt khác, ban đầu vật đang có li độ âm và động năng đang tăng nên ${{x}_{o}}=-\dfrac{A\sqrt{2}}{2}$ theo chiều dương
$\Rightarrow \varphi =-\dfrac{3\pi }{4}\Rightarrow x=5\cos \left( 4\pi t-\dfrac{3\pi }{4} \right)(cm).$
Đáp án A.