Câu hỏi: Một thùng rượu có bán kính đáy là thiết diện vuông góc với trục và cách đều hai đáy có bán kính là 40 cm, chiều cao thùng rượu là 1m (hình vẽ). Biết rằng mặt phẳng chứa trục và cắt mặt xung quanh thùng rượu là các đường parabol, hỏi thể tích của thùng rượu (đơn vị lít) là bao nhiêu?

A. 425162 lít
B. 212581 lít
C. 212,6 lít
D. 425,2 lít
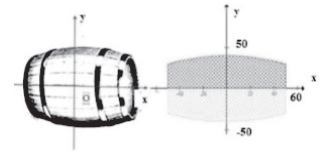
Gọi parabol nằm trên là
Khi đó parabol đi qua điểm có tọa độ
Đổi 1m = 100cm và bán kính đáy là 30cm nên ta có
Từ đó
Suy ra
Phương trình Parabol
Thể tích thùng rượu là

A. 425162 lít
B. 212581 lít
C. 212,6 lít
D. 425,2 lít
Gọi parabol nằm trên là
Khi đó parabol đi qua điểm có tọa độ
Đổi 1m = 100cm và bán kính đáy là 30cm nên ta có
Từ đó
Suy ra
Phương trình Parabol
Thể tích thùng rượu là
| Chú ý: Khi tính tích phân ở bước cuối các em bấm máy tính để tiết kiệm thời gian. |
Đáp án D.