Câu hỏi: Một sợi dây AB dài 24 cm, hai đầu cố định, đang có sóng dừng với hai bụng sóng. Khi dây duỗi thẳng, M và N là hai điểm trên dây chia sợi dây thành ba đoạn bằng nhau. Tỉ số khoảng cách lớn nhất và nhỏ nhất giữa hai điểm M và N trong quá trình sợi dây dao động là 1,25. Biên độ dao động của bụng sóng là
A. 4 cm.
B. 5 cm.
C. 2
D. 3
A. 4 cm.
B. 5 cm.
C. 2
D. 3
+
+ Dây duỗi thẳng:
+ M và N ngược pha (thuộc 2 bó sóng liên tiếp)
M0N0 = 1,25MN = 10cm
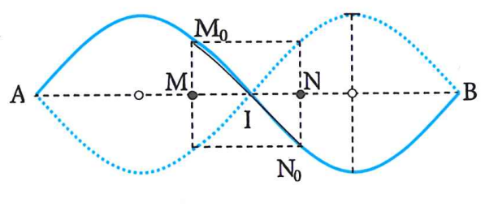
+ Dây duỗi thẳng:
+ M và N ngược pha (thuộc 2 bó sóng liên tiếp)
M0N0 = 1,25MN = 10cm
Đáp án C.