Google
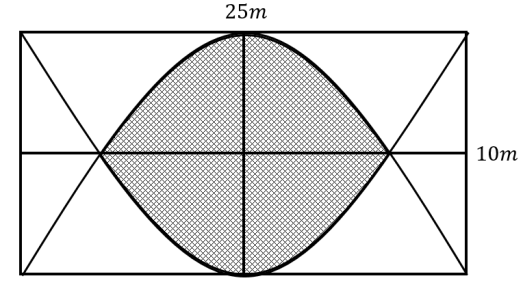
Câu hỏi: Một mảnh vườn toán học có dạng hình chữ nhật, chiều dài là $25m$ và chiều rộng là $10m$. Các nhà Toán học dùng hai đường parabol, mỗi parabol có đỉnh là trung điểm của một cạnh dài và đi qua 2 điểm đầu của cạnh đối diện, phần mảnh vườn nằm ở miền trong của cả hai parabol (phần gạch sọc như hình vẽ minh họa) được trồng hoa Hồng. Biết chi phí để trồng hoa Hồng là 35.000đồng $/{{m}^{2}}$. Số tiền các nhà Toán học phải chi để trồng hoa trên phần mảnh vườn đó? (Số tiền được làm tròn đến hàng nghìn).
A. $4.124.000$ đồng.
B. $3.300.000$ đồng.
C. $5.185.000$ đồng.
D. $4.243.000$ đồng.
B. $3.300.000$ đồng.
C. $5.185.000$ đồng.
D. $4.243.000$ đồng.
Đặt hệ trục tọa độ như hình vẽ bên dưới.
Parabol $P\left( x \right)$ đi qua các điểm $O\left( 0;0 \right)$, $A\left( 12.5;10 \right)$ và đạt cực trị tại $x=0$ có dạng $y=P\left( x \right)=a{{x}^{2}} \left( a>0 \right)$. Dễ dàng tìm được hàm số $y=P\left( x \right)=\dfrac{8}{125}{{x}^{2}} $.
Gọi $E,F$ lần lượt là hai giao điểm của hai parabol (hình vẽ). Hoành độ điểm $F$ là nghiệm phương trình hoành độ giao điểm của $y=P\left( x \right)$ và đường thẳng $y=5$
$\left\{ \begin{aligned}
& \dfrac{8}{125}{{x}^{2}} =5 \\
& x>0 \\
\end{aligned} \right.\Leftrightarrow {{x}_{F}}=\dfrac{25\sqrt{2}}{4}$.
Nhận xét, diện tích cần tìm được chia thành 4 phần bằng nhau, trong đó diện tích một phần được tính như sau: ${{S}_{1}}=\int\limits_{0}^{{{x}_{F}}}{\left( 5-P\left( x \right) \right)}dx=\int\limits_{0}^{\dfrac{25\sqrt{2}}{4}}{\left( 5-\dfrac{8}{125}{{x}^{2}} \right)}dx \approx 29.46278\left( {{m}^{2}} \right)$.
Vậy số tiền các nhà Toán học phải chi để trồng hoa trên phần mảnh vườn đó bằng:
$4\times {{S}_{1}}\times 35.000=4\times 29.46278\times 35.000=4.124.789$ đồng.
Gọi $E,F$ lần lượt là hai giao điểm của hai parabol (hình vẽ). Hoành độ điểm $F$ là nghiệm phương trình hoành độ giao điểm của $y=P\left( x \right)$ và đường thẳng $y=5$
$\left\{ \begin{aligned}
& \dfrac{8}{125}{{x}^{2}} =5 \\
& x>0 \\
\end{aligned} \right.\Leftrightarrow {{x}_{F}}=\dfrac{25\sqrt{2}}{4}$.
Nhận xét, diện tích cần tìm được chia thành 4 phần bằng nhau, trong đó diện tích một phần được tính như sau: ${{S}_{1}}=\int\limits_{0}^{{{x}_{F}}}{\left( 5-P\left( x \right) \right)}dx=\int\limits_{0}^{\dfrac{25\sqrt{2}}{4}}{\left( 5-\dfrac{8}{125}{{x}^{2}} \right)}dx \approx 29.46278\left( {{m}^{2}} \right)$.
Vậy số tiền các nhà Toán học phải chi để trồng hoa trên phần mảnh vườn đó bằng:
$4\times {{S}_{1}}\times 35.000=4\times 29.46278\times 35.000=4.124.789$ đồng.
Đáp án A.