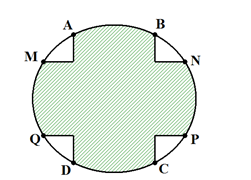
Câu hỏi: Một mảnh vườn hoa dạng hình tròn có bán kính bằng $5m $. Phần đất trồng hoa là phần tô trong hình vẽ bên. Kinh phí trồng hoa là $50.000$ đồng/ ${{m}^{2}}$. Hỏi số tiền cần để trồng hoa trên diện tích phần đất đó là bao nhiêu, biết hai hình chữ nhật $ABCD$ và $MNPQ$ có $AB=MQ=5m$ ?
A. $\text{3}\text{.641}\text{.528}$ đồng.
B. $\text{3}\text{.533}\text{.057}$ đồng.
C. $3.641.529$ đồng.
D. $\text{3}\text{.533}\text{.058}$ đồng.

Đặt hệ trục $Oxy$ như hình vẽ.
Phương trình đường tròn ${{x}^{2}}+{{y}^{2}}=25\Leftrightarrow y=\pm \sqrt{25-{{x}^{2}}}$.
Tìm được tọa độ điểm $N\left( \dfrac{5\sqrt{3}}{2};\dfrac{5}{2} \right)$ (một giao điểm của đường tròn và đường thẳng $y=\dfrac{5}{2}$ ).
Diện tích 4 phần trắng (không trồng cây) là: ${{S}_{1}}=4\int\limits_{\dfrac{5}{2}}^{\dfrac{5\sqrt{3}}{2}}{\left( \sqrt{25-{{x}^{2}}}-\dfrac{5}{2} \right)}\text{d}x$.
Diện tích phần trồng rau bằng diện tích hình tròn trừ cho ${{S}_{1}}$, tức là $S=\pi {{r}^{2}}-{{S}_{1}}=\pi {{.5}^{2}}-4\int\limits_{\dfrac{5}{2}}^{\dfrac{5\sqrt{3}}{2}}{\left( \sqrt{25-{{x}^{2}}}-\dfrac{5}{2} \right)}\text{d}x$ $=25\pi -4\left( \dfrac{25\pi }{12}-\dfrac{5}{2}.\left( \dfrac{5\sqrt{3}}{2}-\dfrac{5}{2} \right) \right)=\dfrac{50\pi }{3}+25\sqrt{3}-25$.
Số tiền cần để trồng hoa là: $50000.S\approx 3533057$ đồng.

A. $\text{3}\text{.641}\text{.528}$ đồng.
B. $\text{3}\text{.533}\text{.057}$ đồng.
C. $3.641.529$ đồng.
D. $\text{3}\text{.533}\text{.058}$ đồng.
Đặt hệ trục $Oxy$ như hình vẽ.
Phương trình đường tròn ${{x}^{2}}+{{y}^{2}}=25\Leftrightarrow y=\pm \sqrt{25-{{x}^{2}}}$.
Tìm được tọa độ điểm $N\left( \dfrac{5\sqrt{3}}{2};\dfrac{5}{2} \right)$ (một giao điểm của đường tròn và đường thẳng $y=\dfrac{5}{2}$ ).
Diện tích 4 phần trắng (không trồng cây) là: ${{S}_{1}}=4\int\limits_{\dfrac{5}{2}}^{\dfrac{5\sqrt{3}}{2}}{\left( \sqrt{25-{{x}^{2}}}-\dfrac{5}{2} \right)}\text{d}x$.
Diện tích phần trồng rau bằng diện tích hình tròn trừ cho ${{S}_{1}}$, tức là $S=\pi {{r}^{2}}-{{S}_{1}}=\pi {{.5}^{2}}-4\int\limits_{\dfrac{5}{2}}^{\dfrac{5\sqrt{3}}{2}}{\left( \sqrt{25-{{x}^{2}}}-\dfrac{5}{2} \right)}\text{d}x$ $=25\pi -4\left( \dfrac{25\pi }{12}-\dfrac{5}{2}.\left( \dfrac{5\sqrt{3}}{2}-\dfrac{5}{2} \right) \right)=\dfrac{50\pi }{3}+25\sqrt{3}-25$.
Số tiền cần để trồng hoa là: $50000.S\approx 3533057$ đồng.
Đáp án B.