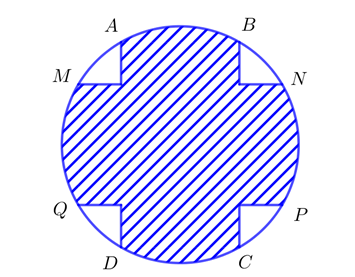
Câu hỏi: Một mảnh vườn hoa có dạng hình tròn bán kính bằng $5m.$ Phần đất trồng hoa là phần tô trong hình vẽ bên. Kinh phí để trồng hoa là $50.000$ đồng/ ${{m}^{2}}.$ Hỏi số tiền cần để trồng hoa trên diện tích phần đất đó là bao nhiêu, biết hai hình chữ nhật $ABCD$ và $MNPQ$ có $AB=MQ=5m?$
A. $3.533.058$ đồng.
B. $3.641.528$ đồng.
C. $3.641.529$ đồng.
D. $3.533.057$ đồng.

Đặt hệ trục Oxy như hình vẽ, mảnh vườn sẽ có phương trình $(C):{{x}^{2}}+{{y}^{2}}=25$.
Diện tích hình phẳng giới hạn vởi (C), AD, BC là: ${{S}_{1}}=4\int\limits_{0}^{5/2}{\sqrt{25-{{x}^{2}}}\text{d}x=\dfrac{25\pi }{3}+\dfrac{25\sqrt{3}}{2}}$.
Diện tích hình phẳng giới hạn vởi (C), MN, QP là: ${{S}_{2}}={{S}_{1}}$ (do tính đối xứng)
Diện tích phần đất trồng hoa (phần tô trong hình vẽ) là:
$S={{S}_{1}}+{{S}_{2}}-{{S}_{IJLKL}}=2(\dfrac{25\pi }{3}+\dfrac{25\sqrt{3}}{2})-25$.
Số tiền cần để trồng hoa trên diện tích phần đất đó là: $S.50000\approx 3.533.057$ đồng.

A. $3.533.058$ đồng.
B. $3.641.528$ đồng.
C. $3.641.529$ đồng.
D. $3.533.057$ đồng.
Đặt hệ trục Oxy như hình vẽ, mảnh vườn sẽ có phương trình $(C):{{x}^{2}}+{{y}^{2}}=25$.
Diện tích hình phẳng giới hạn vởi (C), AD, BC là: ${{S}_{1}}=4\int\limits_{0}^{5/2}{\sqrt{25-{{x}^{2}}}\text{d}x=\dfrac{25\pi }{3}+\dfrac{25\sqrt{3}}{2}}$.
Diện tích hình phẳng giới hạn vởi (C), MN, QP là: ${{S}_{2}}={{S}_{1}}$ (do tính đối xứng)
Diện tích phần đất trồng hoa (phần tô trong hình vẽ) là:
$S={{S}_{1}}+{{S}_{2}}-{{S}_{IJLKL}}=2(\dfrac{25\pi }{3}+\dfrac{25\sqrt{3}}{2})-25$.
Số tiền cần để trồng hoa trên diện tích phần đất đó là: $S.50000\approx 3.533.057$ đồng.
Đáp án D.