Câu hỏi: Một khu vườn dạng hình tròn có hai đường kính AB, CD vuông góc với nhau,

A.
B.
C.
D.
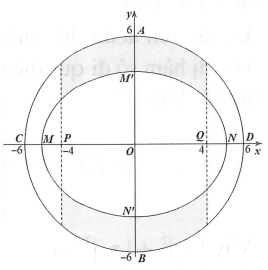
Đặt hệ trục tọa độ như hình vẽ. Ta có
Phương trình đường tròn là
Phương trình elip là:
Khi đó diện tích phần trồng cỏ là:

A.
B.
C.
D.
Đặt hệ trục tọa độ như hình vẽ. Ta có
Phương trình đường tròn là
Phương trình elip là:
Khi đó diện tích phần trồng cỏ là:
Đáp án D.