Câu hỏi: Một hộp đựng Chocolate bằng kim loại có hình dạng lúc mở nắp như hình vẽ dưới đây. Một phần tư thể tích phía trên hộp được rải một lớp bơ sữa ngọt, phần còn lại phía dưới chứa đầy chocolate nguyên chất. Với kích thước như hình vẽ, gọi

A.
B.
C.
D.

A.
B.
C.
D.
ĐK:
Thể tích hộp kim loại là
Đặt
Ta có:
Ta có bảng biến thiên của
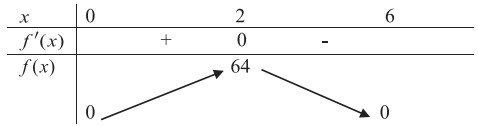
Vậy giá trị lớn nhất của V là 64
Tuy nhiên thể tích sôcôla nguyên chất chỉ chiếm
Thể tích hộp kim loại là
Đặt
Ta có:
Ta có bảng biến thiên của
Vậy giá trị lớn nhất của V là 64
Tuy nhiên thể tích sôcôla nguyên chất chỉ chiếm
Đáp án D.