Câu hỏi: . Một con lắc lò xo thẳng đứng gồm một vật nặng khối lượng m = 100 g và lò xo có độ cứng k = 20 N/m. Vật nặng được đặt trên giá đỡ nằm ngang sao cho lò xo không biến dạng. Cho giá đỡ đi xuống không vận tốc đầu với gia tốc a = 2,0 m/s2. Bỏ qua mọi ma sát và lực cản, lấy g = 10 m/s2. Ở thời điểm lò xo dài nhất lần đầu tiên, khoảng cách giữa vật nặng và giá đỡ gần giá trị nào nhất sau đây?
A. 4,0 cm.
B. 3,7 cm.
C. 3,0 cm.
D. 4,2 cm.
A. 4,0 cm.
B. 3,7 cm.
C. 3,0 cm.
D. 4,2 cm.
+ Mấu chốt của bài toán ta phải tìm được vị trí vật rời khỏi giá đỡ → sau đó vật sẽ dao động điều hòa.
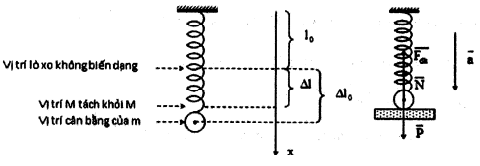
+ Chọn trục Ox theo phương thẳng đứng, gốc O trùng với vị trí cân bằng của con lắc lò xo, có chiều dương hướng xuống.
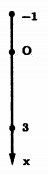
+ Các lực tác dụng lên vật trong quá trình chuyển động cùng giá đỡ là: $\overrightarrow{P},\overrightarrow{N},\overrightarrow{{{F}_{dh}}}$ (như hình vẽ)
+ Áp dụng định luật II Niuton cho vật: $\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{{{F}_{dh}}}=m\overrightarrow{a}$ (1)
Chiếu $\xrightarrow{(1)}Ox:P-N-{{F}_{dh}}=ma$
+ Khi vật m rời khỏi giá đỡ thì $N=0\leftrightarrow P-{{F}_{dh}}=ma\to {{F}_{dh}}=mg-ma=0,8N$.
→ Độ dãn của lò xo khi đó là $\Delta \ell =\dfrac{{{F}_{dh}}}{k}=0,04m=4cm$.
+ Sau khi rời lò xo bắt đầu dao động điều hòa xung quanh vị trí cân bằng O
$(\Delta {{\ell }_{0}}=\dfrac{mg}{k}=0,05m=5cm)$
→ Li độ của vật tại vị trí rời giá đỡ: $x=-\left( 5-4 \right)=-1\ cm$
+ Vận tốc của vật tại vị trí rời: ${{v}^{2}}-v_{0}^{2}=2as\leftrightarrow {{v}^{2}}-0=2.2.0,04\to v=0,4\text{ m/s}=40\text{ cm/s}$.
+ Tần số góc dao động con lắc: $\omega =\sqrt{\dfrac{k}{m}}=10\sqrt{2}\text{ rad/s}$.
→ Biên độ dao động của con lắc là: $A=\sqrt{\dfrac{{{v}^{2}}}{{{\omega }^{2}}}+{{x}^{2}}}=3cm$.
+ Quãng đường vật m đi từ vị trí rời ( $x=-1$ ) → vị trí lò xo dãn cực đại ( $+A=3$ ) là:
${{S}_{1}}=1+3=4cm$.
+ Thời gian vật m đi từ vị trí rời ( $x=-1$ ) → vị trí lò xo dãn cực đại ( $+A=3$ ) là:
$t=\dfrac{\arcsin \left( \dfrac{1}{3} \right)+\dfrac{\pi }{2}}{10\sqrt{2}}=0,135\text{s}$.
+ Quãng đường giá đỡ đi được từ vị trí rời đến khi lò xo dãn cực đại:
${{S}_{2}}={{v}_{0}}t+\dfrac{1}{2}a{{t}^{2}}=40.0,135+\dfrac{1}{2}.200.0,{{135}^{2}}=7,23\ cm$.
→ Khoảng cách giá đỡ và vật khi đó là: $\Delta d=7,23-4=3,23\ cm$.
+ Chọn trục Ox theo phương thẳng đứng, gốc O trùng với vị trí cân bằng của con lắc lò xo, có chiều dương hướng xuống.
+ Các lực tác dụng lên vật trong quá trình chuyển động cùng giá đỡ là: $\overrightarrow{P},\overrightarrow{N},\overrightarrow{{{F}_{dh}}}$ (như hình vẽ)
+ Áp dụng định luật II Niuton cho vật: $\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{{{F}_{dh}}}=m\overrightarrow{a}$ (1)
Chiếu $\xrightarrow{(1)}Ox:P-N-{{F}_{dh}}=ma$
+ Khi vật m rời khỏi giá đỡ thì $N=0\leftrightarrow P-{{F}_{dh}}=ma\to {{F}_{dh}}=mg-ma=0,8N$.
→ Độ dãn của lò xo khi đó là $\Delta \ell =\dfrac{{{F}_{dh}}}{k}=0,04m=4cm$.
+ Sau khi rời lò xo bắt đầu dao động điều hòa xung quanh vị trí cân bằng O
$(\Delta {{\ell }_{0}}=\dfrac{mg}{k}=0,05m=5cm)$
→ Li độ của vật tại vị trí rời giá đỡ: $x=-\left( 5-4 \right)=-1\ cm$
+ Vận tốc của vật tại vị trí rời: ${{v}^{2}}-v_{0}^{2}=2as\leftrightarrow {{v}^{2}}-0=2.2.0,04\to v=0,4\text{ m/s}=40\text{ cm/s}$.
+ Tần số góc dao động con lắc: $\omega =\sqrt{\dfrac{k}{m}}=10\sqrt{2}\text{ rad/s}$.
→ Biên độ dao động của con lắc là: $A=\sqrt{\dfrac{{{v}^{2}}}{{{\omega }^{2}}}+{{x}^{2}}}=3cm$.
+ Quãng đường vật m đi từ vị trí rời ( $x=-1$ ) → vị trí lò xo dãn cực đại ( $+A=3$ ) là:
${{S}_{1}}=1+3=4cm$.
+ Thời gian vật m đi từ vị trí rời ( $x=-1$ ) → vị trí lò xo dãn cực đại ( $+A=3$ ) là:
$t=\dfrac{\arcsin \left( \dfrac{1}{3} \right)+\dfrac{\pi }{2}}{10\sqrt{2}}=0,135\text{s}$.
+ Quãng đường giá đỡ đi được từ vị trí rời đến khi lò xo dãn cực đại:
${{S}_{2}}={{v}_{0}}t+\dfrac{1}{2}a{{t}^{2}}=40.0,135+\dfrac{1}{2}.200.0,{{135}^{2}}=7,23\ cm$.
→ Khoảng cách giá đỡ và vật khi đó là: $\Delta d=7,23-4=3,23\ cm$.
Đáp án C.