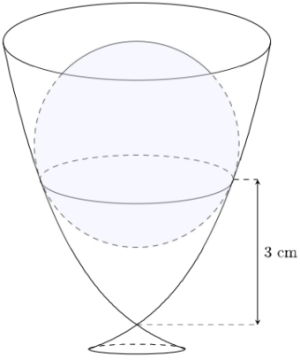
Câu hỏi: Một chiếc ly bằng thủy tinh đang chứa nước bên trong được tạo thành khi quay một phần đồ thị hàm số
A.
B.
C.
D.
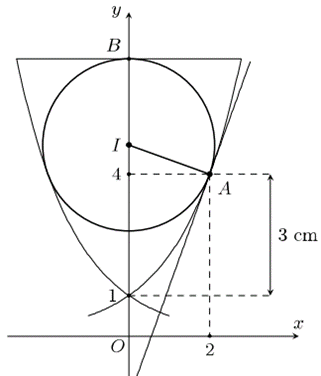
Xét mặt phẳng
Tiếp tuyến với
Đường thẳng vuông góc với
Tâm
Ta có
Dung tích chiếc ly là
Thể tích nước chứa trong chiếc ly là

A.
B.
C.
D.
Xét mặt phẳng
Tiếp tuyến với
Đường thẳng vuông góc với
Tâm
Ta có
Dung tích chiếc ly là
Thể tích nước chứa trong chiếc ly là
Đáp án A.