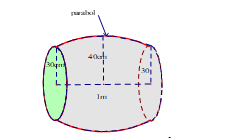
Câu hỏi: Một cái trống trường có bán kính các đáy là $30$ cm, thiết diện vuông góc với trục và cách đều hai đáy có diện tích là $1600\pi \left( c{{m}^{2}} \right)$, chiều dài của trống là $1m$. Biết rằng mặt phẳng chứa trục cắt mặt xung quanh của trống là các đường Parabol. Hỏi thể tích của cái trống là bao nhiêu?
 .
.
A. $425,2$ (lít).
B. $425162$ (lít).
C. $212,6$ (lít).
D. $212581$ (lít).
 .
.A. $425,2$ (lít).
B. $425162$ (lít).
C. $212,6$ (lít).
D. $212581$ (lít).
Ta có chọn hệ trục $Oxy$ như hình vẽ.
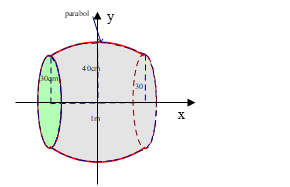
Thiết diện vuông góc với trục và cách đều hai đáy là hình tròn.
có bán kính $r$ có diện tích là $1600\pi \left( c{{m}^{2}} \right)$, nên.
${{r}^{2}}\pi =1600\pi \Rightarrow r=40cm$.
Ta có: Parabol có đỉnh $I\left( 0; 40 \right)$ và qua $A\left( 50; 30 \right)$.
Nên có phương trình $y=-\dfrac{1}{250}{{x}^{2}}+40$.
Thể tích của trống là.
$V=\pi \int\limits_{-50}^{50}{{{\left( -\dfrac{1}{250}{{x}^{2}}+40 \right)}^{2}}dx}=\pi .\dfrac{406000}{3}c{{m}^{3}}\approx 425,2d{{m}^{3}}=425,2$ (lít)
Thiết diện vuông góc với trục và cách đều hai đáy là hình tròn.
có bán kính $r$ có diện tích là $1600\pi \left( c{{m}^{2}} \right)$, nên.
${{r}^{2}}\pi =1600\pi \Rightarrow r=40cm$.
Ta có: Parabol có đỉnh $I\left( 0; 40 \right)$ và qua $A\left( 50; 30 \right)$.
Nên có phương trình $y=-\dfrac{1}{250}{{x}^{2}}+40$.
Thể tích của trống là.
$V=\pi \int\limits_{-50}^{50}{{{\left( -\dfrac{1}{250}{{x}^{2}}+40 \right)}^{2}}dx}=\pi .\dfrac{406000}{3}c{{m}^{3}}\approx 425,2d{{m}^{3}}=425,2$ (lít)
Đáp án A.