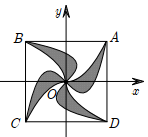
Mặt sàn của một thang máy có dạng hình vuông $ABCD$ cạnh $2m$ được lát gạch màutrắng và trang trí bởi một hình 4 cánh giống nhau màu sẫm. Khi đặt...

Phương pháp:
- Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f\left( x \right),y=g\left( x \right),$ đường thẳng $x=a,x=b$ là $S=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|dx}.$ Từ đó tính diện tích 1 cánh của hình trang trí và suy ra diện tích hình trang trí.
- Sử dụng dữ kiện diện tích trang trí màu sẫm chiếm $\dfrac{1}{3}$ diện tích mặt sàn suy ra 1 phương trình bậc nhất 2 ẩn $a,b.$
- Sử dụng: Đồ thị hàm số $y=a{{x}^{3}}+bx$ đi qua điểm $A\left( 1;1 \right)$ suy ra thêm 1 phương trình bậc nhất 2 ẩn $a,b.$
- Giải hệ tìm $a,b$ và tính $ab.$
Cách giải:
Diện tích 1 cánh của hình trang trí là ${{S}_{1}}=\int\limits_{0}^{1}{\left( {{x}^{2}}-a{{x}^{3}}-bx \right)dx}=\left( \dfrac{{{x}^{3}}}{3}-\dfrac{a{{x}^{4}}}{4}-\dfrac{b{{x}^{2}}}{2} \right)\left| \begin{aligned}
& 1 \\
& 0 \\
\end{aligned} \right.=\dfrac{1}{3}-\dfrac{a}{4}-\dfrac{b}{2}.$
$\Rightarrow $ Diện tích hình trang trí là $S=4{{S}_{1}}=\dfrac{4}{3}-a-2b.$
Vì diện tích trang trí màu sẫm chiếm $\dfrac{1}{3}$ diện tích mặt sàn nên $\dfrac{4}{3}-a-2b=\dfrac{4}{3}\Leftrightarrow a+2b=0.$
Đồ thị hàm số $y=a{{x}^{3}}+bx$ đi qua điểm $A\left( 1;1 \right)$ nên $a+b=1.$
Khi đó ta có $\left\{ \begin{aligned}
& a+2b=0 \\
& a+b=1 \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& a=2 \\
& b=-1 \\
\end{aligned} \right..$
Vậy $ab=-2.$