Hỏi có bao nhiêu số nguyên dương $a, a\le 2023$ sao cho tồn tại số...

Điều kiện xác định: $x>0; a>1; a\in \mathbb{N}$.
Bất phương trình đã cho $\Leftrightarrow x.\ln a+x.{{e}^{x}}\le {{e}^{x}}+{{e}^{x}}.\ln \left( x\ln a \right)$. Đặt $t=\ln \left( x\ln a \right)\Leftrightarrow {{e}^{t}}=x.\ln a$
Khi đó, bất phương trình trở thành: ${{e}^{t}}+x.{{e}^{x}}\le {{e}^{x}}+{{e}^{x}}.t\Leftrightarrow {{e}^{t-x}}+x\le 1+t$.
Đặt $u=t-x$ suy ra ${{e}^{u}}\le 1+u\Leftrightarrow {{e}^{u}}-1-u\le 0 \left( 1 \right)$.
Xét hàm số $f\left( u \right)={{e}^{u}}-1-u; {f}'\left( u \right)={{e}^{u}}-1$
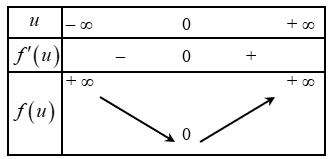Từ bảng biến thiên suy ra $f\left( u \right)\ge 0$ với mọi $u$ nên $\left( 1 \right)\Leftrightarrow u=0\Leftrightarrow t=x$.
Khi đó: ${{e}^{x}}=x.\ln a\Leftrightarrow \ln a=\dfrac{{{e}^{x}}}{x}$. Xét hàm số $g\left( x \right)=\dfrac{{{e}^{x}}}{x}; {g}'\left( x \right)=\dfrac{{{e}^{x}}\left( x-1 \right)}{{{x}^{2}}}$
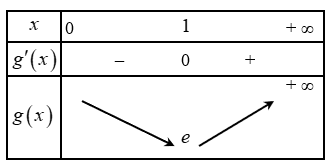Bất phương trình đã cho có nghiệm khi và chỉ khi $\ln a\ge e\Leftrightarrow a\ge {{e}^{e}}\approx 15,15$.
Vậy $a\in \!\!\{\!\!\text{ 16;17;}...\text{;2023}\}$ nên có $2008$ giá trị thỏa mãn yêu cầu bài toán.