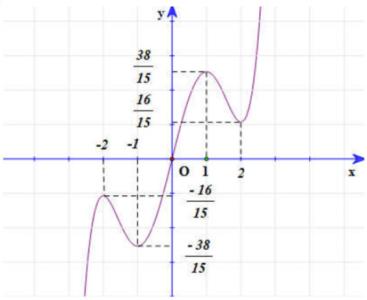
Hàm số nào $y=f\left( x \right)$ có đồ thị như hình bên dưới. Đồ...

Đặt $g\left( x \right)=\left| h\left( x \right) \right|$.
Nhận xét: Số cực trị hàm $g\left( x \right)$ bằng số cực trị hàm số $h\left( x \right)$ cộng với số giao điểm cắt của đồ thị hàm số $h\left( x \right)$ với trục hoành.
$h\left( x \right)=0\Leftrightarrow f\left( x \right)=-\dfrac{1}{15}$.
Dựa vào đồ thị hàm số $f\left( x \right)$ suy ra phương trình $f\left( x \right)=-\dfrac{1}{15}$ có một nghiệm đơn thuộc $\left( -1;0 \right)$ suy ra đồ thị hàm số $h\left( x \right)$ cắt trục hoành tại 1 điểm thuộc $\left( -1;0 \right)$.
Ta có ${h}'\left( x \right)=15{f}'\left( x \right)$ ; ${h}'\left( x \right)=0\Leftrightarrow {f}'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=-2 \\
& x=-1 \\
& x=1 \\
& x=2 \\
\end{aligned} \right.$.
Các nghiệm $x=\pm 1; x=\pm 2$ đều là các nghiệm đơn suy ra $h\left( x \right)$ có bốn cực trị.
Vậy $g\left( x \right)=\left| h\left( x \right) \right|$ có năm cực trị.