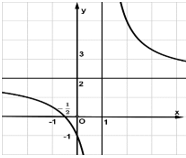
Câu hỏi: Đường cong ở hình bên dưới là đồ thị của hàm số $y=\dfrac{ax+b}{cx+d}$ với $a,b,c,d$ là các số thực. Giá trị nhỏ nhất của hàm số trên đoạn $\left[ -1;0 \right]$ là
A. $-1$
B. 1
C. 0
D. 2

A. $-1$
B. 1
C. 0
D. 2
Phương pháp:
Dựa vào đồ thị xác định điểm thấp nhất của đồ thị trên $\left[ -1;0 \right].$
Cách giải:
Ta thấy trên đoạn $\left[ -1;0 \right]$ đồ thị hàm số hướng xuống hay hàm số nghịch biến nên $\underset{\left[ -1;0 \right]}{\mathop{\min }} y=y\left( 0 \right)=-1.$
Dựa vào đồ thị xác định điểm thấp nhất của đồ thị trên $\left[ -1;0 \right].$
Cách giải:
Ta thấy trên đoạn $\left[ -1;0 \right]$ đồ thị hàm số hướng xuống hay hàm số nghịch biến nên $\underset{\left[ -1;0 \right]}{\mathop{\min }} y=y\left( 0 \right)=-1.$
Đáp án D.