Google
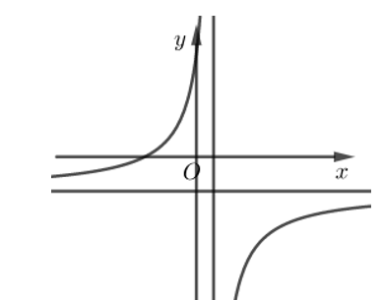
Câu hỏi: Đồ thị của hàm số nào dưới đây có dạng như đường cong hình dưới?
A. $y=\dfrac{2x+3}{2x-1}$.
B. $y=\dfrac{2x-3}{1-2x}$.
C. $y=\dfrac{2x+3}{1-2x}$.
D. $y=\dfrac{2x+3}{x-1}$.
$y=\dfrac{ax+b}{cx+d} \left( c\ne 0.ad-bc\ne 0 \right)$.
Đồ thị hàm số có đường tiệm cận ngang nằm phía dưới trục hoành nên $\dfrac{a}{c}<0$.
B. $y=\dfrac{2x-3}{1-2x}$.
C. $y=\dfrac{2x+3}{1-2x}$.
D. $y=\dfrac{2x+3}{x-1}$.
Dễ thấy đồ thị hàm số đã cho là đồ thị hàm số phân thức hữu tỉ dạng$y=\dfrac{ax+b}{cx+d} \left( c\ne 0.ad-bc\ne 0 \right)$.
Đồ thị hàm số có đường tiệm cận ngang nằm phía dưới trục hoành nên $\dfrac{a}{c}<0$.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ âm nên loại đáp ánB.
Suy ra hàm số cần tìm là $y=\dfrac{2x+3}{1-2x}$.Đáp án C.