Câu hỏi: Diện tích phần mặt phẳng bị giới hạn bởi đồ thị hàm số
A. 3,53
B. 2,824
C. 4,612
D. 5,237
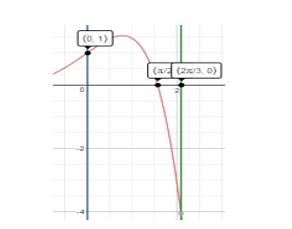
Giao điểm của đồ thị
Diện tích phần hình phẳng giới hạn bởi 4 đường trên là:
Bài toán này ta cần chú ý
Ta có:
Suy ra
Tương tự ta có:
A. 3,53
B. 2,824
C. 4,612
D. 5,237
Giao điểm của đồ thị
Diện tích phần hình phẳng giới hạn bởi 4 đường trên là:
Bài toán này ta cần chú ý
Ta có:
Suy ra
Tương tự ta có:
Đáp án B.