Google
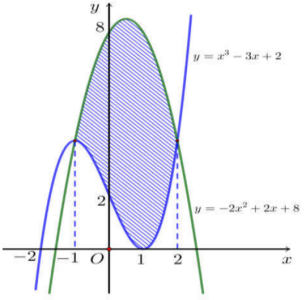
Câu hỏi: Diện tích hình phẳng phần gạch chéo trong hình vẽ bên được tính theo công thức nào sau đây?
A. $S=\int\limits_{-1}^{2}{\left( {{x}^{3}}+2{{x}^{2}}-5x-6 \right)\text{d}x}$.
B. $S=\int\limits_{-1}^{2}{\left( {{x}^{3}}+2{{x}^{2}}-x-10 \right)\text{d}x}$.
C. $S=\int\limits_{-1}^{2}{\left( {{x}^{3}}-2{{x}^{2}}-x+10 \right)\text{d}x}$.
D. $S=\int\limits_{-1}^{2}{\left( -{{x}^{3}}-2{{x}^{2}}+5x+6 \right)\text{d}x}$.
B. $S=\int\limits_{-1}^{2}{\left( {{x}^{3}}+2{{x}^{2}}-x-10 \right)\text{d}x}$.
C. $S=\int\limits_{-1}^{2}{\left( {{x}^{3}}-2{{x}^{2}}-x+10 \right)\text{d}x}$.
D. $S=\int\limits_{-1}^{2}{\left( -{{x}^{3}}-2{{x}^{2}}+5x+6 \right)\text{d}x}$.
Ta có: $S=\int\limits_{-1}^{2}{\left| \left( {{x}^{3}}-3x+2 \right)-\left( -2{{x}^{2}}+2x+8 \right) \right|} \text{d}x$
$=\int\limits_{-1}^{2}{\left[ \left( -2{{x}^{2}}+2x+8 \right)-\left( {{x}^{3}}-3x+2 \right) \right]} \text{d}x$ (Vì $-2{{x}^{2}}+2x+8\ge {{x}^{3}}-3x+2, \forall x\in \left[ -1 ; 2 \right]$ ).
$=\int\limits_{-1}^{2}{\left( -{{x}^{3}}-2{{x}^{2}}+5x+6 \right)} \text{d}x$.
Vậy diện tích hình phẳng phần gạch chéo trong hình vẽ là $S=\int\limits_{-1}^{2}{\left( -{{x}^{3}}-2{{x}^{2}}+5x+6 \right)} \text{d}x$.
$=\int\limits_{-1}^{2}{\left[ \left( -2{{x}^{2}}+2x+8 \right)-\left( {{x}^{3}}-3x+2 \right) \right]} \text{d}x$ (Vì $-2{{x}^{2}}+2x+8\ge {{x}^{3}}-3x+2, \forall x\in \left[ -1 ; 2 \right]$ ).
$=\int\limits_{-1}^{2}{\left( -{{x}^{3}}-2{{x}^{2}}+5x+6 \right)} \text{d}x$.
Vậy diện tích hình phẳng phần gạch chéo trong hình vẽ là $S=\int\limits_{-1}^{2}{\left( -{{x}^{3}}-2{{x}^{2}}+5x+6 \right)} \text{d}x$.
Đáp án D.