Google
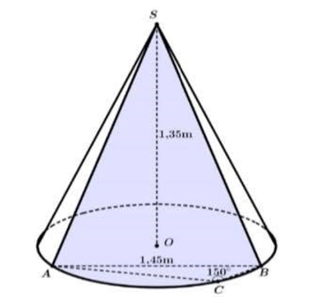
Câu hỏi: Cửa hàng $A$ có đặt trước sảnh một cái nón lớn với chiều cao $1,35m$ và sơn cách điệu hoa văn trang trí một phần mặt ngoài của hình nón ứng với cung nhỏ $AB$ như hình vẽ. Biết $AB=1,34m, \overset\frown{ACB}=150{}^\circ $ và giá tiền trang trí là $2.000.000$ đồng mỗi mét vuông. Hỏi số tiền mà cửa hàng $A$ cần dùng để trang trí là bao nhiêu?
A. $4.215.000$ đồng.
B. $4.510.000$ đồng.
C. $3.021.000$ đồng.
D. $3.008.000$ đồng.
Dựng đường kính $AM$, $I$ là hình chiếu vuông góc của $O$ lên $AB$.
Do $\overset\frown{ACB}=150{}^\circ \Rightarrow $ Số đo cung lớn: $s \overset\frown{AB}=300{}^\circ $
Ta có $s \overset\frown{AB}=s \overset\frown{AM}+s \overset\frown{MB}\Rightarrow s\overset\frown{MB}=120{}^\circ \Rightarrow \overset\frown{OAI}=60{}^\circ $
Xét $\vartriangle OAI$ có $R=0A=\dfrac{AI}{\cos \overset\frown{OAI}}=\dfrac{0,725}{\cos 60{}^\circ }=1,45 m$
Khi đó $SA=\sqrt{S{{O}^{2}}+O{{A}^{2}}}\approx 1,981 m$
Diện tích xung quanh của khối nón: ${{S}_{xq}}=2\pi .SA.OA=\pi .1,981.1,45=9,024 m$
Diện tích phần trang trí: $S=\left( 1-\dfrac{300}{360} \right).{{S}_{xq}}=1,504 \left( {{m}^{2}} \right)$
Số tiền cửa hàng cần phải trả: $1,504.2000000=3.008.000$ đồng.
B. $4.510.000$ đồng.
C. $3.021.000$ đồng.
D. $3.008.000$ đồng.
Do $\overset\frown{ACB}=150{}^\circ \Rightarrow $ Số đo cung lớn: $s \overset\frown{AB}=300{}^\circ $
Ta có $s \overset\frown{AB}=s \overset\frown{AM}+s \overset\frown{MB}\Rightarrow s\overset\frown{MB}=120{}^\circ \Rightarrow \overset\frown{OAI}=60{}^\circ $
Xét $\vartriangle OAI$ có $R=0A=\dfrac{AI}{\cos \overset\frown{OAI}}=\dfrac{0,725}{\cos 60{}^\circ }=1,45 m$
Khi đó $SA=\sqrt{S{{O}^{2}}+O{{A}^{2}}}\approx 1,981 m$
Diện tích xung quanh của khối nón: ${{S}_{xq}}=2\pi .SA.OA=\pi .1,981.1,45=9,024 m$
Diện tích phần trang trí: $S=\left( 1-\dfrac{300}{360} \right).{{S}_{xq}}=1,504 \left( {{m}^{2}} \right)$
Số tiền cửa hàng cần phải trả: $1,504.2000000=3.008.000$ đồng.
Đáp án D.