Câu hỏi: Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số
A. 6.
B. 4.
C. 3.
D. 5.
A. 6.
B. 4.
C. 3.
D. 5.
Ta có:
TH1:
Do đó
TH2:
Hàm số đồng biến trên khoảng
Xét hàm số
TH1:
Bảng biến thiên:
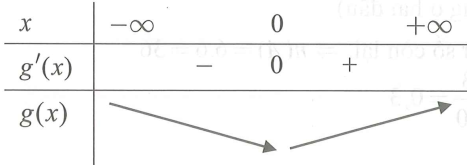
Từ bảng biến thiên
TH2:
Vậy
TH1:
Do đó
TH2:
Hàm số đồng biến trên khoảng
Xét hàm số
TH1:
Bảng biến thiên:
Từ bảng biến thiên
TH2:
Vậy
Đáp án A.