Google
Câu hỏi: Có bao nhiêu số nguyên $x$ thỏa mãn $\left( {{2}^{{{x}^{2}}+2x+2}}-{{4}^{x+3}} \right)\left( {{\log }_{2}}\left( {{x}^{3}}+12{{x}^{2}}+45x+54 \right)-2 \right)\le 0$ ?
A. $5$.
B. $6$.
C. $7$.
D. $8$.
A. $5$.
B. $6$.
C. $7$.
D. $8$.
Điều kiện của bất phương trình: ${{x}^{3}}+12{{x}^{2}}+45x+54>0\Leftrightarrow (x+6){{(x+3)}^{2}}>0\Leftrightarrow \left\{ \begin{aligned}
& x>-6 \\
& x\ne -3 \\
\end{aligned} \right.$.
Ta có: ${{2}^{{{x}^{2}}+2x+2}}-{{4}^{x+3}}=0\Leftrightarrow {{x}^{2}}+2x+2=2(x+3)\Leftrightarrow x=\pm 2$.
${{\log }_{2}}\left( {{x}^{3}}+12{{x}^{2}}+45x+54 \right)-2=0$ $\Leftrightarrow {{x}^{3}}+12{{x}^{2}}+45x+54=4$
$\Leftrightarrow {{(x+5)}^{2}}(x+2)=0\Leftrightarrow \left[ \begin{aligned}
& x=-5 \\
& x=-2 \\
\end{aligned} \right.$.
Bảng xét dấu của vế trái (VT) bất phương trình đã cho
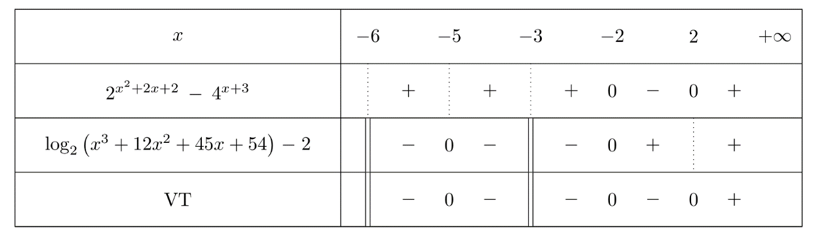Từ bảng xét dấu, ta được tập nghiệm của bất phương trình là $S=\left( -6\ ;\ -3 \right)\cup \left( -3\ ;\ 2 \right]$.
Vậy có tất cả $7$ số nguyên $x$ thỏa mãn yêu cầu là: $-5$ ; $-4$ ; $-2$ ; $-1$ ; $0$ ; $1$ ; $2$.
& x>-6 \\
& x\ne -3 \\
\end{aligned} \right.$.
Ta có: ${{2}^{{{x}^{2}}+2x+2}}-{{4}^{x+3}}=0\Leftrightarrow {{x}^{2}}+2x+2=2(x+3)\Leftrightarrow x=\pm 2$.
${{\log }_{2}}\left( {{x}^{3}}+12{{x}^{2}}+45x+54 \right)-2=0$ $\Leftrightarrow {{x}^{3}}+12{{x}^{2}}+45x+54=4$
$\Leftrightarrow {{(x+5)}^{2}}(x+2)=0\Leftrightarrow \left[ \begin{aligned}
& x=-5 \\
& x=-2 \\
\end{aligned} \right.$.
Bảng xét dấu của vế trái (VT) bất phương trình đã cho
Vậy có tất cả $7$ số nguyên $x$ thỏa mãn yêu cầu là: $-5$ ; $-4$ ; $-2$ ; $-1$ ; $0$ ; $1$ ; $2$.
Đáp án C.
