Có bao nhiêu số nguyên dương $x$ sao cho tồn tại số thực $y$ lớn...

Điều kiện: $\left\{ \begin{matrix}
2y-x+3>0 \\
y>1 \\
x\ge 1 \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
x-2y<3 \\
y>1 \\
x\ge 1 \\
\end{matrix} \right.$
$\left( x{{y}^{2}}+x-2y-1 \right)\log y=\log \dfrac{2y-x+3}{x}$
$\Leftrightarrow \left( x{{y}^{2}}+x-2y-1 \right)\log y-2\log y=\log \dfrac{2y-x+3}{x}-2\log y$
$\Leftrightarrow \left( x{{y}^{2}}+x-2y-3 \right)\log y=\log \dfrac{2y-x+3}{x{{y}^{2}}}$
$\Leftrightarrow \left( a-b \right)\log y=\log \dfrac{b}{a}\Leftrightarrow \left( a-b \right)\log y+\log \dfrac{a}{b}=0$, với $\left\{ \begin{matrix}
a=x{{y}^{2}} \\
b=2y-x+3 \\
\end{matrix} \right.\left( a,b>0 \right)$
Nếu $a>b$ thì $\left( a-b \right)\log y+\log \dfrac{a}{b}>0$, $a<b$ thì $\left( a-b \right)\log y+\log \dfrac{a}{b}<0$.
Nên $\left( a-b \right)\log y+\log \dfrac{a}{b}=0\Leftrightarrow a=b$ $\Leftrightarrow x{{y}^{2}}=2y-x+3$ $\Leftrightarrow x=\dfrac{2y+3}{{{y}^{2}}+1}$.
Xét hàm số $f\left( y \right)=\dfrac{2y+3}{{{y}^{2}}+1}$ với $y>1$. Ta có ${f}'\left( y \right)=\dfrac{-2{{y}^{2}}-6y+2}{{{\left( {{y}^{2}}+1 \right)}^{2}}}<0,\forall y>1$.
Nên $f\left( y \right)$ nghịch biến trên $\left( 1;+\infty \right)$.
Bảng biến thiên:
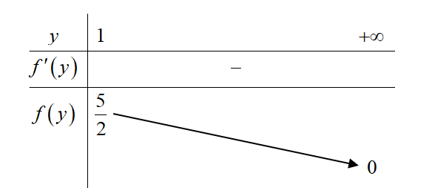Để tồn tại số thực $y$ lớn hơn $1$ thì $0<x<\dfrac{5}{2}\Rightarrow x\in \left\{ 1;2 \right\}$.