Có bao nhiêu số nguyên $a$ để tồn tại số phức $z$ thỏa mãn $\left|...

Đặt $z=x+yi \left( x;y\in \mathbb{R} \right)\Rightarrow \overline{z}=x-yi$.
Ta có $\left| z+\bar{z} \right|+\left| z-\bar{z} \right|=16\Leftrightarrow 2\left| x \right|+2\left| y \right|=16\Leftrightarrow \left| x \right|+\left| y \right|=8$
$\Leftrightarrow \left\{ \begin{aligned}
& x+y=8\left( {{d}_{1}} \right), khi x\ge 0;y\ge 0 \\
& x-y=8\left( {{d}_{2}} \right), khi x\ge 0;y\le 0 \\
& -x-y=8\left( {{d}_{3}} \right), khi x\le 0;y\le 0 \\
& -x+y=8\left( {{d}_{4}} \right), khi x\le 0;y\ge 0 \\
\end{aligned} \right. \left( 1 \right)$
Hay điểm $M\left( x;y \right)$ biểu diễn số phức $z$ nằm trên các cạnh của hình vuông ABCD như hình.
Lại có $\left| iz-4 \right|=a\Leftrightarrow \left\{ \begin{aligned}
& a\ge 0 \\
& \left| -y-4+xi \right|=a \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& a\ge 0 \\
& {{x}^{2}}+{{\left( y+4 \right)}^{2}}={{a}^{2}} \\
\end{aligned} \right. \left( 2 \right)$
TH1: nếu $a=0\Rightarrow \left\{ \begin{aligned}
& x=0 \\
& y=-4 \\
\end{aligned} \right.$ không thỏa mãn điều kiện (1) (loại).
TH2: Nếu $a>0$ điểm $M\left( x;y \right)$ biểu diễn số phức $z$ nằm trên đường tròn tâm $I\left( 0;-4 \right)$ bán kính $a$.
Để tồn tại số phức $z$ thỏa cả hai điều kiện $\left( 1 \right)$ và $\left( 2 \right)$ thì hình vuông $ABCD$ và đường tròn $\left( I;a \right)$ phải có điểm chung
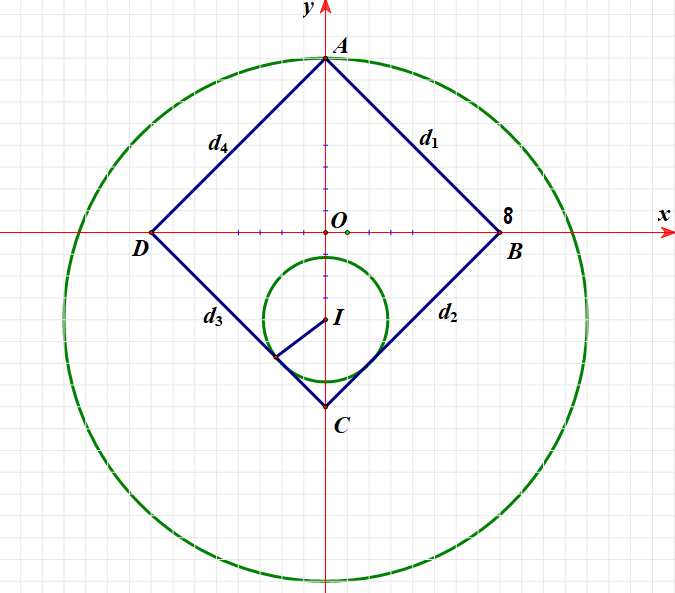Do đó $d\left( I;{{d}_{3}} \right)\le a\le IA\Leftrightarrow 2\sqrt{2}\le a\le 12\overset{a\in \mathbb{Z}}{\mathop{\Rightarrow }} a\in \left\{ 3;4;5;...;12 \right\}$
Vậy có 10 số nguyên thỏa mãn.