Google
Câu hỏi: Có bao nhiêu giá trị nguyên của tham số $m$ để tập nghiệm của bất phương trình ${{\log }_{2}}\left( {{x}^{2}}+2x+{{2}^{m}} \right)-2{{\log }_{2}}\left( 2x-1 \right)\ge 0$ chứa đúng hai nghiệm nguyên.
A. $10$.
B. $9$.
C. $4$.
D. $3$.
A. $10$.
B. $9$.
C. $4$.
D. $3$.
Ta có: ${{\log }_{2}}\left( {{x}^{2}}+2x+{{2}^{m}} \right)-2{{\log }_{2}}\left( 2x-1 \right)\ge 0\Leftrightarrow {{\log }_{2}}\left( {{x}^{2}}+2x+{{2}^{m}} \right)\ge 2{{\log }_{2}}\left( 2x-1 \right)$
$\Leftrightarrow \left\{ \begin{aligned}
& 2x-1>0 \\
& {{x}^{2}}+2x+{{2}^{m}}\ge {{\left( 2x-1 \right)}^{2}} \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& x>\dfrac{1}{2} \\
& {{2}^{m}}\ge 3{{x}^{2}}-6x+1 \\
\end{aligned} \right.$.
Xét hàm số $f\left( x \right)=3{{x}^{2}}-6x+1$ trên $\left( \dfrac{1}{2};+\infty \right)$, ta có ${f}'\left( x \right)=6x-6; {f}'\left( x \right)=0\Leftrightarrow x=1$.
Bảng biến thiên
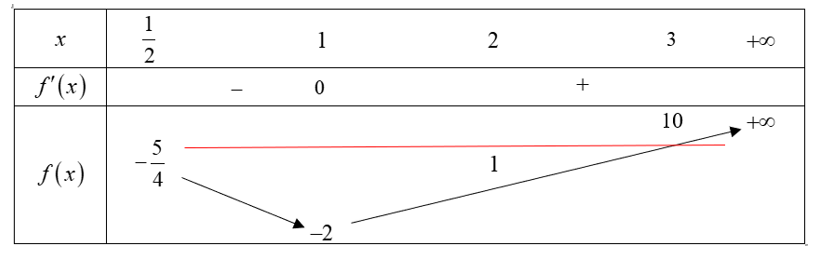Yêu cầu bài toán $\Leftrightarrow 1\le {{2}^{m}}<10\Leftrightarrow 0\le m<{{\log }_{2}}10$, $m\in \mathbb{Z}\Rightarrow m\in \left\{ 0;1;2;3 \right\}$.
Vậy có $4$ giá trị nguyên của $m$ thỏa mãn yêu cầu bài toán.
$\Leftrightarrow \left\{ \begin{aligned}
& 2x-1>0 \\
& {{x}^{2}}+2x+{{2}^{m}}\ge {{\left( 2x-1 \right)}^{2}} \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& x>\dfrac{1}{2} \\
& {{2}^{m}}\ge 3{{x}^{2}}-6x+1 \\
\end{aligned} \right.$.
Xét hàm số $f\left( x \right)=3{{x}^{2}}-6x+1$ trên $\left( \dfrac{1}{2};+\infty \right)$, ta có ${f}'\left( x \right)=6x-6; {f}'\left( x \right)=0\Leftrightarrow x=1$.
Bảng biến thiên
Vậy có $4$ giá trị nguyên của $m$ thỏa mãn yêu cầu bài toán.
Đáp án C.