Bài toán
Cho hệ dao đông như hình vẽ
. Vật có khối lượng $m=100g$; lò xo có độ cứng $k=40 \ \text{N}/\text{m}$. Kéo vật xuống phía dưới theo phương thẳng đứng $3cm$; rồi truyền cho vật vận tốc $30 \ \left(\text{cm}/\text{s}\right)$ hướng lên.
1) chứng minh vật dao động điều hòa. Viết phương trình dao động của vật(chọn gốc tọa độ ở vị trí cân bằng; chiều dương như hình vẽ; gốc thời gian khi vật bắt đầu chuyển động). Bỏ qua khối lượng ròng rọc; lò xo; dây; và bỏ qua mọi ma sát. Lấy $g=10 \ \left(\text{m}/\text{s}^{2}\right)$
2)tìm lực căng dây; lực đàn hồi của lò xo khi vật xuống thấp nhất.
3)tìm cơ năng của hệ và li độ của vật khi động năng bằng 3 thế năng(gốc tính thế năng tại vị trí cân băng của vật).
$\textbf{a:}$ Tại vị trí cân bằng, xét cân bằng của ròng rọc và của vật nặng, ta có $$\dfrac{k\Delta l_0}{2}=mg$$
Xét hệ tại thời điểm mà vật m đang nằm bên dưới điểm O một đoạn bằng x. Chọn gốc thế năng tại vị trí cân bằng.
Động năng của hệ: $$E_{\text{đ}}=\dfrac{1}{2}mv^2$$
Thế năng của hệ: $$E_t=\dfrac{1}{2}k\left(\Delta l_0+\dfrac{x}{2}\right)^2-mgx$$
Cơ năng của hệ: $$E=\dfrac{1}{2}mv^2+\dfrac{1}{2}k\left(\Delta l_0+\dfrac{x}{2}\right)^2-mgx$$
Vì bỏ qua ma sát và lực cản nên cơ năng của hệ được bảo toàn, khi đó $$\dfrac{dE}{dt}=0$$
$$\Leftrightarrow mv^{'}v+\dfrac{kx^{'}}{2}\left(\Delta l_0+\dfrac{x}{2}\right)-mgx^{'}=0$$
Ta lại có: $v=x^{'}$, $v^{'}=x^{''}$ và tại thời điểm khảo sát vật có vận tốc khác không nên ta suy ra $$mx^{''}+\dfrac{kx}{4}+\dfrac{k\Delta l_0}{2}-mg=0$$ $$\Leftrightarrow mx^{''}+\dfrac{kx}{4}=0$$ $$\Leftrightarrow x^{''}+\dfrac{kx}{4m}=0$$
Đặt $$\omega ^2=\dfrac{k}{4m}$$
ta có $$x^{''}+\omega ^2x=0$$
Phương trình vi phân này chứng tỏ vật m dao động điều hòa và có chu kỳ $$T=2\pi \sqrt{\dfrac{4m}{k}}=...$$
Phương trình dao động của vật có dạng $$x=A\cos \left(\omega t+\varphi \right)$$
Trong đó $$\omega =\sqrt{\dfrac{k}{4m}}=\sqrt{\dfrac{40}{4.0,1}}=10\quad \left(\dfrac{rad}{s}\right)$$
Tại vị trí ban đầu, ta có $$A=\sqrt{x^2+\dfrac{v^2}{\omega ^2}}=\sqrt{3^2+\dfrac{30^2}{10^2}}=3\sqrt{2} \quad \left(cm\right)$$
Tại vị trí ban đầu $t=0$, ta có $$x=3\sqrt{2}\cos \varphi=3\qquad \Rightarrow \qquad \cos \varphi=\dfrac{1}{\sqrt{2}}$$
và $v<0$, ta suy ra $\varphi=\dfrac{\pi }{4}$.
Vậy phương trình dao động của vật là $$x=3\sqrt{2}\cos \left(10t+\dfrac{\pi }{4}
\right)\quad \left(cm\right)$$
$\textbf{b:}$ Khi vật ở vị trí thấp nhất thì lò xo giãn một đoạn là $$\Delta l=\Delta l_0+\dfrac{A}{2}=\dfrac{2mg}{k}+\dfrac{A}{2}=...=0,07m$$
Lực đàn hồi của lò xo: $$F_{\text{đh}}=k\Delta l=40.0,07=2,85N$$
Lực căng dây trên mỗi nhánh dây: $$T=\dfrac{F_{\text{đh}}}{2}=1,425N$$
$\textbf{c:}$ Câu này có vẻ quen thuộc nhỉ! Chỉ lưu ý là công thức tính thế năng trong trường hợp này được xác định bằng biểu thức $$E_t=\dfrac{1}{2}m\omega ^2x^2$$
.....................................
Tôi hay sử dụng phương pháp Năng lượng để khảo sát dao động của hệ. Phương pháp Động lực học thầy Tân dùng là đúng rồi đó em. Ròng rọc khối lượng không đáng kể, có thể xem bằng không nên có hệ phương trình động lực học như vậy.
Google
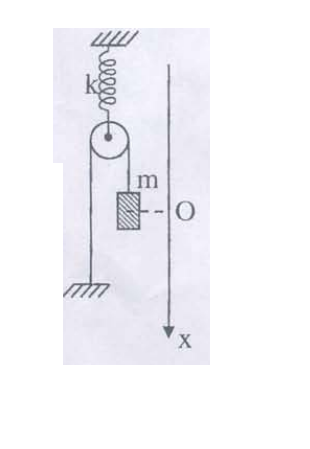. Vật có khối lượng $m=100g$; lò xo có độ cứng $k=40 \ \text{N}/\text{m}$. Kéo vật xuống phía dưới theo phương thẳng đứng $3cm$; rồi truyền cho vật vận tốc $30 \ \left(\text{cm}/\text{s}\right)$ hướng lên.
