Google
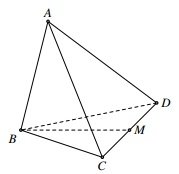
Câu hỏi: Cho tứ diện đều $ABCD.$ Gọi M là trung điểm của CD. Côsin của góc giữa hai đường thẳng AC và BM bằng
A. $\dfrac{\sqrt{3}}{6}.$
B. $\dfrac{\sqrt{3}}{2}.$
C. $\dfrac{\sqrt{3}}{3}.$
D. $\sqrt{3}.$
B. $\dfrac{\sqrt{3}}{2}.$
C. $\dfrac{\sqrt{3}}{3}.$
D. $\sqrt{3}.$
Gọi N là trung điểm $AD\Rightarrow MN//AC\Rightarrow \widehat{\left( AC;BM \right)}=\widehat{BMN}.$
Ta có $BM=BN=\dfrac{a\sqrt{3}}{2};MN=\dfrac{a}{2}\Rightarrow \cos \widehat{BMN}=\dfrac{B{{M}^{2}}+M{{N}^{2}}-B{{N}^{2}}}{2BM.MN}=\dfrac{\sqrt{3}}{6}.$ Chọn A.
Ta có $BM=BN=\dfrac{a\sqrt{3}}{2};MN=\dfrac{a}{2}\Rightarrow \cos \widehat{BMN}=\dfrac{B{{M}^{2}}+M{{N}^{2}}-B{{N}^{2}}}{2BM.MN}=\dfrac{\sqrt{3}}{6}.$ Chọn A.
Đáp án A.