Google
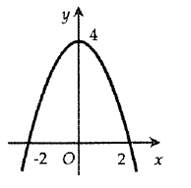
Câu hỏi: Cho Parabol như hình vẽ bên. Diện tích hình phẳng giới hạn bởi Parabol và trục hoành bằng
A. $\dfrac{32}{3}$.
B. $16.$
C. $\dfrac{16}{3}$.
D. $\dfrac{28}{3}$.
Dựa vào Parabol như hình vẽ, suy ra phương trình của Parabol là $\left( P \right):y=a{{x}^{2}}+4$ ; $\left( P \right)$ cắt trục hoành tại các điểm có hoành độ $\pm 2$ nên $a=-1$ $\Rightarrow \left( P \right):y=-{{x}^{2}}+4.$
Do đó, diện tích hình phẳng giới hạn bởi Parabol và trục hoành bằng
A. $\dfrac{32}{3}$.
B. $16.$
C. $\dfrac{16}{3}$.
D. $\dfrac{28}{3}$.
Do đó, diện tích hình phẳng giới hạn bởi Parabol và trục hoành bằng
$S=\int\limits_{-2}^{2}{\left( -{{x}^{2}}+4 \right)dx}=2\int\limits_{0}^{2}{\left( -{{x}^{2}}+4 \right)dx}=2\left( -\dfrac{{{x}^{3}}}{3}+4x \right)\left| _{\begin{smallmatrix}
\\
0
\end{smallmatrix}}^{\begin{smallmatrix}
2 \\
\end{smallmatrix}}=\dfrac{32}{3}. \right.$
Đáp án A.