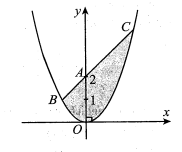
Câu hỏi: Cho parabol
A.
B.
C.
D.

A.
B.
C.
D.
Đường thẳng đi qua điểm A có phương trình là
Phương trình hoành độ giao điểm giữa parabol và đường thẳng là:
Giả sử
Từ giả thiết:

Do đó
Phương trình hoành độ giao điểm giữa parabol và đường thẳng là:
Giả sử
Từ giả thiết:
Do đó
Đáp án B.