Google
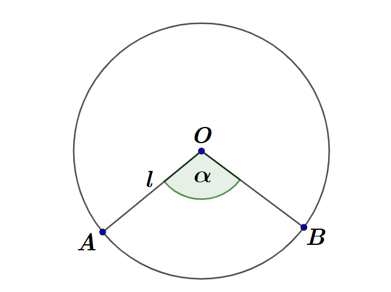
Câu hỏi: Cho một miếng tôn hình tròn tâm $O$, bán kính $R$. Cắt bỏ một phần miếng tôn theo một hình quạt $OAB$ và gò phần còn lại thành một hình nón đỉnh $O$ không có đáy $(OA$ trùng với $OB)$. Tìm số đo góc ở tâm của mảnh tôn cắt bỏ để thể tích của khối nón đạt giá trị lớn nhất.
A. $\dfrac{2\sqrt{6}\pi }{3}$
B. $\left( 2-\dfrac{\sqrt{6}}{3} \right)\pi $
C. $\left( 2-\dfrac{2\sqrt{6}}{3} \right)\pi $
D. $\dfrac{\sqrt{6}\pi }{3}$
Ta có thể tích khối nón là $V=\dfrac{1}{3}h\pi {{r}^{2}}=\dfrac{\pi }{3}\sqrt{{{l}^{2}}-{{r}^{2}}}{{r}^{2}}$
Với $l$ cố định, $V=\sqrt{\dfrac{{{\pi }^{2}}}{18}\left( 2{{l}^{2}}-2{{r}^{2}} \right){{r}^{2}}{{r}^{2}}}\le \sqrt{\dfrac{{{\pi }^{2}}}{18}\dfrac{{{\left( 2{{l}^{2}}-2{{r}^{2}}+{{r}^{2}}+{{r}^{2}} \right)}^{3}}}{27}}=\dfrac{2\pi \sqrt{3}}{27}{{l}^{3}}$
Đẳng thức xảy $\Leftrightarrow 2{{l}^{2}}-2{{r}^{2}}={{r}^{2}}\Leftrightarrow r=\dfrac{\sqrt{6}}{3}l$.
Đặt $OA=l$ là bán đường kính đường tròn tâm $O$ và là đường sinh của hình nón được tạo ra khi gò phần còn lại của miếng tôn sau khi cắt bỏ hình quạt $OAB$.
Gọi $S$ là diện tích xung quanh của hình nón, khi đó $S=\pi O{{A}^{2}}\left( 1-\dfrac{\alpha }{2\pi } \right)=\pi {{l}^{2}}\left( 1-\dfrac{\alpha }{2\pi } \right)$.
Mặt khác gọi $r$ là bán kính hình nón, khi đó $r=\dfrac{S}{\pi l}=l\left( 1-\dfrac{\alpha }{2\pi } \right)$.
Áp dụng chứng minh trên ta có được $r=l\left( 1-\dfrac{\alpha }{2\pi } \right)=\dfrac{\sqrt{6}}{3}l\Leftrightarrow 1-\dfrac{\alpha }{2\pi }=\dfrac{\sqrt{6}}{3}\Leftrightarrow \alpha =\left( 2-\dfrac{2\sqrt{6}}{3} \right)\pi $.
A. $\dfrac{2\sqrt{6}\pi }{3}$
B. $\left( 2-\dfrac{\sqrt{6}}{3} \right)\pi $
C. $\left( 2-\dfrac{2\sqrt{6}}{3} \right)\pi $
D. $\dfrac{\sqrt{6}\pi }{3}$
Với $l$ cố định, $V=\sqrt{\dfrac{{{\pi }^{2}}}{18}\left( 2{{l}^{2}}-2{{r}^{2}} \right){{r}^{2}}{{r}^{2}}}\le \sqrt{\dfrac{{{\pi }^{2}}}{18}\dfrac{{{\left( 2{{l}^{2}}-2{{r}^{2}}+{{r}^{2}}+{{r}^{2}} \right)}^{3}}}{27}}=\dfrac{2\pi \sqrt{3}}{27}{{l}^{3}}$
Đẳng thức xảy $\Leftrightarrow 2{{l}^{2}}-2{{r}^{2}}={{r}^{2}}\Leftrightarrow r=\dfrac{\sqrt{6}}{3}l$.
Đặt $OA=l$ là bán đường kính đường tròn tâm $O$ và là đường sinh của hình nón được tạo ra khi gò phần còn lại của miếng tôn sau khi cắt bỏ hình quạt $OAB$.
Gọi $S$ là diện tích xung quanh của hình nón, khi đó $S=\pi O{{A}^{2}}\left( 1-\dfrac{\alpha }{2\pi } \right)=\pi {{l}^{2}}\left( 1-\dfrac{\alpha }{2\pi } \right)$.
Mặt khác gọi $r$ là bán kính hình nón, khi đó $r=\dfrac{S}{\pi l}=l\left( 1-\dfrac{\alpha }{2\pi } \right)$.
Áp dụng chứng minh trên ta có được $r=l\left( 1-\dfrac{\alpha }{2\pi } \right)=\dfrac{\sqrt{6}}{3}l\Leftrightarrow 1-\dfrac{\alpha }{2\pi }=\dfrac{\sqrt{6}}{3}\Leftrightarrow \alpha =\left( 2-\dfrac{2\sqrt{6}}{3} \right)\pi $.
Đáp án C.
