Câu hỏi: Cho mặt cầu tâm
A.
B.
C.
D.
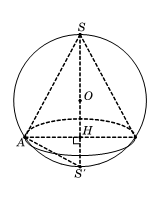
Gọi
Tam giác
A.
B.
C.
D.
Gọi
Tam giác
Đáp án C.