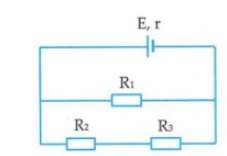
Câu hỏi: Cho mạch điện như hình vẽ. Biết $E=12V;r=1\Omega ;{{R}_{1}}=5\Omega ;{{R}_{2}}={{R}_{3}}=10\Omega _{{}}^{{}}$ Bỏ qua điện trở của dây nối. Hiệu điện thế giữa hai đầu R1 là
A. 7,6V
B. 4,8V
C. 9,6V
D. 10,2V

A. 7,6V
B. 4,8V
C. 9,6V
D. 10,2V
Phương pháp:
Áp dụng định luật Ôm tính cường độ dòng điện chạy trong mạch: $I=\dfrac{E}{r+{{R}_{N}}}$
Sử dụng các công thức của đoạn mạch nối tiếp và song song.
Hiệu điện thế hai đầu mạch ngoài: U = E - Ir .
Cách giải:
Mạch ngoài gồm: R 1 / / ( R 2 nt R 3 )
Điện trở tương đương của mạch ngoài:
$\dfrac{1}{{{R}_{N}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{23}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}+{{R}_{3}}}=\dfrac{1}{5}+\dfrac{1}{20}=\dfrac{1}{4}\Rightarrow {{R}_{N}}=4\Omega $
Cường độ dòng điện chạy trong mạch: $I=\dfrac{E}{r+{{R}_{N}}}=\dfrac{12}{1+4}=2,4A$
Hiệu điện thế giữa hai đầu R1 là : U 1 = U = E – I.r = 12 - 2,4.1 = 9,6 V
Áp dụng định luật Ôm tính cường độ dòng điện chạy trong mạch: $I=\dfrac{E}{r+{{R}_{N}}}$
Sử dụng các công thức của đoạn mạch nối tiếp và song song.
Hiệu điện thế hai đầu mạch ngoài: U = E - Ir .
Cách giải:
Mạch ngoài gồm: R 1 / / ( R 2 nt R 3 )
Điện trở tương đương của mạch ngoài:
$\dfrac{1}{{{R}_{N}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{23}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}+{{R}_{3}}}=\dfrac{1}{5}+\dfrac{1}{20}=\dfrac{1}{4}\Rightarrow {{R}_{N}}=4\Omega $
Cường độ dòng điện chạy trong mạch: $I=\dfrac{E}{r+{{R}_{N}}}=\dfrac{12}{1+4}=2,4A$
Hiệu điện thế giữa hai đầu R1 là : U 1 = U = E – I.r = 12 - 2,4.1 = 9,6 V
Đáp án C.