Google
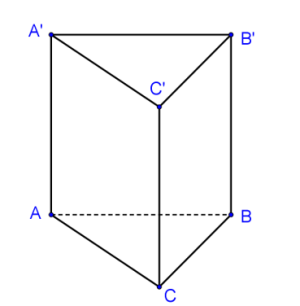
Câu hỏi: Cho lăng trụ tam giác đều có tất cả các cạnh bằng $a$, $\tan $ của góc giữa mặt phẳng $({A}'BC)$ và mặt đáy $(ABC)$ bằng
A. $\dfrac{\sqrt{2}}{3}$.
B. $\dfrac{2}{\sqrt{3}}$.
C. $\dfrac{3}{\sqrt{2}}$.
D. $\dfrac{\sqrt{3}}{2}$.
Gọi $M$ là trung điểm của $BC$, khi đó $AM\bot BC$ và $AM=\dfrac{a\sqrt{3}}{2}$.
Ta có $BC\bot AM$ và $BC\bot A{A}'$ nên $BC\bot ({A}'AM)$. Suy ra $BC\bot {A}'M$.
Vì $({A}'BC)\cap (ABC)=BC$, ${A}'M\bot BC$, $AM\bot BC$ nên góc giữa hai mặt phẳng $({A}'BC)$ và $(ABC)$ là góc giữa ${A}'M$ và $AM$, nghĩa là là góc ${A}'MA$.
$\Delta {A}'AM$ vuông ở $A$ $\Rightarrow \tan \widehat{{A}'MA}=\dfrac{{A}'A}{AM}=\dfrac{a}{\dfrac{a\sqrt{3}}{2}}=\dfrac{2}{\sqrt{3}}$.
B. $\dfrac{2}{\sqrt{3}}$.
C. $\dfrac{3}{\sqrt{2}}$.
D. $\dfrac{\sqrt{3}}{2}$.
Ta có $BC\bot AM$ và $BC\bot A{A}'$ nên $BC\bot ({A}'AM)$. Suy ra $BC\bot {A}'M$.
Vì $({A}'BC)\cap (ABC)=BC$, ${A}'M\bot BC$, $AM\bot BC$ nên góc giữa hai mặt phẳng $({A}'BC)$ và $(ABC)$ là góc giữa ${A}'M$ và $AM$, nghĩa là là góc ${A}'MA$.
$\Delta {A}'AM$ vuông ở $A$ $\Rightarrow \tan \widehat{{A}'MA}=\dfrac{{A}'A}{AM}=\dfrac{a}{\dfrac{a\sqrt{3}}{2}}=\dfrac{2}{\sqrt{3}}$.
Đáp án B.